परिभाषा वास्तविक संख्याओं का एक क्रमित संग्रह (x 1 , x 2 , ... , x n ) n कहलाता है एन-आयामी वेक्टर, और संख्याएँ x i (i = ) - अवयवया निर्देशांक,

उदाहरण। यदि, उदाहरण के लिए, एक निश्चित ऑटोमोबाइल प्लांट को प्रति शिफ्ट में 50 कारें, 100 ट्रक, 10 बसें, कारों के लिए स्पेयर पार्ट्स के 50 सेट और ट्रकों और बसों के लिए 150 सेट का उत्पादन करना है, तो इस संयंत्र के उत्पादन कार्यक्रम को इस रूप में लिखा जा सकता है वेक्टर (50, 100 , 10, 50, 150), जिसमें पांच घटक होते हैं।

अंकन। सदिशों को बोल्ड लोअरकेस अक्षरों या शीर्ष पर बार या तीर वाले अक्षरों द्वारा दर्शाया जाता है, उदाहरण के लिए, एया. दो वैक्टर कहलाते हैं बराबरयदि उनके घटकों की संख्या समान है और उनके संबंधित घटक समान हैं।

वेक्टर घटकों को आपस में बदला नहीं जा सकता, उदाहरण के लिए (3, 2, 5, 0, 1)और (2, 3, 5, 0, 1) विभिन्न वैक्टर।
वैक्टर पर संचालन।काम एक्स= (x 1 , x 2 , ... ,x n) एक वास्तविक संख्या के लिएλ वेक्टर कहा जाता हैλ एक्स= (λ x 1, λ x 2, ..., λ x n)।

जोड़एक्स= (x 1 , x 2 , ... , x n) और वाई= (y 1 , y 2 , ... ,y n) सदिश कहलाता है एक्स + वाई= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).

वैक्टर का स्थान।एन -आयामी वेक्टर अंतरिक्ष आर n को सभी n-आयामी सदिशों के समुच्चय के रूप में परिभाषित किया जाता है, जिसके लिए वास्तविक संख्याओं और जोड़ से गुणन की संक्रियाएँ परिभाषित की जाती हैं।

आर्थिक चित्रण। एन-डायमेंशनल वेक्टर स्पेस का आर्थिक उदाहरण: माल की जगह (चीज़ें). अंतर्गत मालहम कुछ अच्छी या सेवा को समझेंगे जो एक निश्चित समय पर एक निश्चित स्थान पर बिक्री के लिए गई थी। मान लें कि n उपलब्ध वस्तुओं की एक सीमित संख्या है; उपभोक्ता द्वारा खरीदे गए उनमें से प्रत्येक की मात्रा को माल के एक सेट द्वारा दर्शाया गया है

एक्स= (x 1 , x 2 , ..., x n),

जहाँ x i उपभोक्ता द्वारा खरीदे गए i-वें माल की मात्रा को दर्शाता है। हम यह मानेंगे कि सभी वस्तुओं में स्वेच्छ विभाज्यता का गुण होता है, ताकि उनमें से प्रत्येक की कोई भी गैर-ऋणात्मक मात्रा खरीदी जा सके। तब वस्तुओं के सभी संभव समुच्चय वस्तु के स्थान के सदिश होते हैं C = ( एक्स= (x 1 , x 2 , ... , x n)एक्स आई ≥ 0, आई =)।

रैखिक स्वतंत्रता। प्रणाली इ 1 , इ 2 , ... , इएम एन-आयामी वैक्टर कहा जाता है रैखिक रूप से निर्भरअगर ऐसी संख्याएँ हैंλ 1 , λ 2 , ... , λ मी , जिनमें से कम से कम एक अशून्य है, जो समानता को संतुष्ट करता हैλ1 इ 1 + λ2 इ 2+...+λm इएम = 0; अन्यथा, सदिशों की इस प्रणाली को कहा जाता है रैखिक रूप से स्वतंत्र, अर्थात यह समानता तभी संभव है जब सभी . ज्यामितीय भाव रैखिक निर्भरतावैक्टर में आर 3, निर्देशित खंडों के रूप में व्याख्या की गई, निम्नलिखित प्रमेयों की व्याख्या करें।

प्रमेय 1। एक सदिश से मिलकर एक प्रणाली रैखिक रूप से निर्भर है अगर और केवल अगर यह सदिश शून्य है।

प्रमेय 2। दो सदिशों के रैखिक रूप से निर्भर होने के लिए, यह आवश्यक और पर्याप्त है कि वे समरेख (समानांतर) हों।

प्रमेय 3 . तीन सदिशों के रैखिक रूप से निर्भर होने के लिए, यह आवश्यक और पर्याप्त है कि वे समतलीय (एक ही तल में स्थित) हों।

सदिशों के बाएँ और दाएँ त्रिगुण। गैर समतलीय सदिशों का तिगुना ए, बी, सीबुलाया सही, यदि पर्यवेक्षक अपने सामान्य मूल से वैक्टर के सिरों को बायपास करता है ए, बी, सीउस क्रम में दक्षिणावर्त आगे बढ़ना प्रतीत होता है। अन्यथा ए, बी, सी -ट्रिपल छोड़ दिया. सदिशों के सभी दाएँ (या बाएँ) त्रिक कहलाते हैं समान रूप से उन्मुखी।

आधार और निर्देशांक। तिकड़ी इ 1, इ 2 , इ 3 गैर समतलीय सदिशों में आर 3 बुलाया आधार, और स्वयं वैक्टर इ 1, इ 2 , इ 3 - बुनियादी. कोई वेक्टर एआधार वैक्टर के संदर्भ में एक अनूठे तरीके से विस्तारित किया जा सकता है, अर्थात इसे रूप में दर्शाया जा सकता है

ए= एक्स 1 इ 1 + x2 इ 2 + एक्स 3 इ 3, (1.1)

संख्याएँ x 1 , x 2 , x 3 विस्तार (1.1) कहलाती हैं COORDINATESएआधार पर इ 1, इ 2 , इ 3 और निरूपित हैं ए(एक्स 1, एक्स 2, एक्स 3)।

ऑर्थोनॉर्मल आधार। यदि वैक्टर इ 1, इ 2 , इ 3 जोड़े में लंबवत हैं और उनमें से प्रत्येक की लंबाई एक के बराबर है, तो आधार कहा जाता है ऑर्थोनॉर्मल, और निर्देशांक x 1 , x 2 , x 3 - आयताकार।ऑर्थोनॉर्मल आधार के आधार सदिशों को निरूपित किया जाएगा मैं, जे, के।

हम अंतरिक्ष में मान लेंगे आर 3 कार्तीय आयताकार निर्देशांक की सही प्रणाली (0, मैं, जे, के}.

वेक्टर उत्पाद. वेक्टर कला एप्रति वेक्टर बीवेक्टर कहा जाता है सी, जो निम्नलिखित तीन स्थितियों द्वारा निर्धारित किया जाता है:

1. वेक्टर लंबाई सीसंख्यात्मक रूप से सदिशों पर निर्मित समांतर चतुर्भुज के क्षेत्रफल के बराबर एऔर बी,अर्थात।
सी= |ए||बी|पाप ( ए^बी).

2. वेक्टर सीप्रत्येक वेक्टर के लंबवत एऔर बी।

3. वैक्टर ए, बीऔर सी, उसी क्रम में लेकर, एक सही त्रिक बनाएँ।

वेक्टर उत्पाद के लिए सीपदनाम पेश किया गया है सी =[अब] या
सी = ए × बी।

यदि वैक्टर एऔर बीसंरेख हैं, फिर पाप ( क ^ ख) = 0 और [ अब] = 0, विशेष रूप से, [ आ] = 0. orts के वेक्टर उत्पाद: [ आईजे]=क, [जेके] = मैं, [की]=जे.

यदि वैक्टर एऔर बीआधार पर दिया गया मैं, जे, के COORDINATES ए(ए 1, ए 2, ए 3), बी(बी 1, बी 2, बी 3), फिर

मिश्रित कार्य। यदि दो वैक्टरों का क्रॉस उत्पाद एऔर बीस्केलर को तीसरे वेक्टर से गुणा किया जाता है सी,तो तीन वैक्टरों के ऐसे उत्पाद को कहा जाता है मिश्रित उत्पादऔर प्रतीक द्वारा निरूपित किया जाता है ए ई.पू.

यदि वैक्टर ए, बीऔर सीआधार पर मैं, जे, केउनके निर्देशांक द्वारा निर्धारित
ए(ए 1, ए 2, ए 3), बी(बी 1, बी 2, बी 3), सी(सी 1, सी 2, सी 3), फिर

.

मिश्रित उत्पाद की एक सरल ज्यामितीय व्याख्या है - यह एक अदिश राशि है, जो तीन दिए गए वैक्टरों पर निर्मित समानांतर चतुर्भुज के आयतन के बराबर है।

यदि सदिश एक सही त्रिक बनाते हैं, तो उनका मिश्रित गुणनफल संकेतित आयतन के बराबर एक धनात्मक संख्या है; अगर तीन ए, बी, सी -छोड़ दिया, फिर एक ख ग<0 и V = - एक ख ग, इसलिए वी =|ए बी सी|.

पहले अध्याय की समस्याओं में सामना किए गए वैक्टर के निर्देशांक को सही ऑर्थोनॉर्मल आधार के सापेक्ष दिया गया माना जाता है। यूनिट वेक्टर वेक्टर के लिए कोडायरेक्शनल ए,प्रतीक द्वारा दर्शाया गया है एओ प्रतीक आर=ओमबिंदु M के त्रिज्या वेक्टर द्वारा निरूपित, प्रतीक a, AB या|ए|, | एबी |वैक्टर के मॉड्यूल को निरूपित किया जाता है एऔर एबी।

उदाहरण 1.2. सदिशों के बीच का कोण ज्ञात कीजिए ए= 2एम+4एनऔर बी= एम-एन, कहाँ एमऔर एन-यूनिट वैक्टर और कोण के बीच एमऔर एन 120 ओ के बराबर।

समाधान. हमारे पास है: क्योंकि φ = अब/अब, अब =(2एम+4एन) (एम-एन) = 2एम 2 - 4एन 2 +2एम.एन.=
= 2 - 4+2cos120 ओ = - 2 + 2(-0.5) = -3; एक = ; ए 2 = (2एम+4एन) (2एम+4एन) =
= 4एम 2 +16एम.एन.+16एन 2 = 4+16(-0.5)+16=12, इसलिए a = . ख = ; बी 2 =
= (एम-एन)(एम-एन) = एम 2 -2एम.एन.+एन 2 = 1-2(-0.5)+1 = 3, इसलिए b = . अंत में हमारे पास है: क्योंकिφ \u003d -1/2, φ \u003d 120 ओ।

उदाहरण 1.3।वैक्टर को जानना अब(-3,-2.6) और ईसा पूर्व(-2,4,4), त्रिभुज ABC की ऊँचाई AD की गणना करें।

समाधान. त्रिभुज ABC के क्षेत्रफल को S से निरूपित करने पर, हम प्राप्त करते हैं:
एस = 1/2 ई.पू. तब AD=2S/BC, BC== = 6,
एस = 1/2 | एबी ×एसी |. एसी = एबी + बीसी, इसलिए वेक्टर एसीनिर्देशांक हैं
. .

उदाहरण 1.4 . दो वैक्टर दिए गए हैं ए(11,10,2) और बी(4,0,3)। यूनिट वेक्टर खोजें सी,वैक्टर के लिए ऑर्थोगोनल एऔर बीऔर निर्देशित किया ताकि वैक्टरों के ट्रिपल का आदेश दिया जा सके ए, बी, सीठीक था।

समाधान।आइए हम वेक्टर के निर्देशांक को निरूपित करें सी x, y, z के संदर्भ में दिए गए सही ऑर्थोनॉर्मल आधार के संबंध में।

क्योंकि सी ⊥ एसी ⊥बी, वह सीए= 0सीबी= 0. समस्या की स्थिति से, यह आवश्यक है कि c = 1 और एक ख ग >0.

हमारे पास समीकरणों की एक प्रणाली है एक्स, वाई, जेड ढूँढना: 11x +10y + 2z = 0, 4x+3z=0, x 2 + y 2 + z 2 = 0।

सिस्टम के पहले और दूसरे समीकरण से हमें z = -4/3 x, y = -5/6 x मिलता है। तीसरे समीकरण में y और z को प्रतिस्थापित करने पर, हमारे पास होगा: x 2 = 36/125, जहां से
एक्स =± . स्थिति का उपयोग करना ए बी सी > 0, हमें असमानता मिलती है

z और y के व्यंजकों को ध्यान में रखते हुए, हम परिणामी असमानता को 625/6 x > 0 के रूप में फिर से लिखते हैं, जहाँ से यह x>0 का अनुसरण करता है। अतः x = , y = - , z = - ।

इस पाठ में, हम सदिशों के साथ दो और संक्रियाओं को देखेंगे: वैक्टर का क्रॉस उत्पादऔर वैक्टर का मिश्रित उत्पाद (जिन्हें इसकी आवश्यकता है उनके लिए तत्काल लिंक). यह ठीक है, कभी-कभी ऐसा होता है कि पूर्ण सुख के लिए भी वैक्टर का डॉट उत्पादअधिक से अधिक की जरूरत है। ऐसी है वेक्टर एडिक्शन। किसी को यह आभास हो सकता है कि हम विश्लेषणात्मक ज्यामिति के जंगल में जा रहे हैं। यह गलत है। उच्च गणित के इस खंड में आमतौर पर बहुत कम जलाऊ लकड़ी होती है, सिवाय शायद पिनोचियो के लिए। वास्तव में, सामग्री बहुत ही सामान्य और सरल है - शायद ही उससे अधिक कठिन हो अदिश उत्पाद, यहां तक ​​कि कम विशिष्ट कार्य भी होंगे। विश्लेषणात्मक ज्यामिति में मुख्य बात, जैसा कि बहुत से लोग देखेंगे या पहले ही देख चुके हैं, गलत गणना नहीं है। एक जादू की तरह दोहराएं, और आप खुश होंगे =)

यदि वेक्टर कहीं दूर चमकते हैं, जैसे क्षितिज पर बिजली, इससे कोई फर्क नहीं पड़ता, पाठ से शुरू करें डमी के लिए वैक्टरवैक्टर के बारे में बुनियादी ज्ञान को पुनर्स्थापित करने या पुनः प्राप्त करने के लिए। अधिक तैयार पाठक चुनिंदा जानकारी से परिचित हो सकते हैं, मैंने उन उदाहरणों का सबसे पूरा संग्रह एकत्र करने की कोशिश की जो अक्सर पाए जाते हैं व्यावहारिक कार्य

आपको क्या खुश करेगा? जब मैं छोटा था, तो मैं दो या तीन गेंदों को भी हथकंडा दे सकता था। इसने अच्छा काम किया। अब हथकंडा करने की बिल्कुल जरूरत नहीं है, क्योंकि हम विचार करेंगे केवल अंतरिक्ष वैक्टर, और दो निर्देशांक वाले समतल सदिशों को छोड़ दिया जाएगा। क्यों? इस प्रकार इन क्रियाओं का जन्म हुआ - वैक्टर के वेक्टर और मिश्रित उत्पाद परिभाषित होते हैं और त्रि-आयामी अंतरिक्ष में काम करते हैं। पहले से आसान!

इस ऑपरेशन में, उसी तरह जैसे स्केलर उत्पाद में, दो वैक्टर. इसे अविनाशी अक्षर होने दो।

कार्रवाई ही लक्षितइस अनुसार: । अन्य विकल्प भी हैं, लेकिन मैं इस तरह से वैक्टर के क्रॉस उत्पाद को निरूपित करता था वर्ग कोष्ठकएक क्रॉस के साथ।

और तुरंत सवाल: मैं फ़िन वैक्टर का डॉट उत्पाददो वैक्टर शामिल हैं, और यहां दो वैक्टर भी गुणा किए जाते हैं क्या अंतर है? एक स्पष्ट अंतर, सबसे पहले, परिणाम में:

सदिशों के अदिश गुणनफल का परिणाम एक NUMBER है:

वैक्टर के क्रॉस उत्पाद का नतीजा एक वेक्टर है: अर्थात, हम सदिशों को गुणा करते हैं और पुन: सदिश प्राप्त करते हैं। बंद क्लब। दरअसल, इसलिए ऑपरेशन का नाम। विभिन्न शैक्षिक साहित्य में, पदनाम भी भिन्न हो सकते हैं, मैं पत्र का उपयोग करूंगा।

क्रॉस उत्पाद की परिभाषा

पहले चित्र के साथ परिभाषा होगी, फिर टिप्पणियाँ होंगी।

परिभाषा: पार उत्पाद गैर समरेखवैक्टर, इस क्रम में लिया, वेक्टर कहा जाता है, लंबाईजो संख्यात्मक रूप से है समांतर चतुर्भुज के क्षेत्रफल के बराबर, इन सदिशों पर निर्मित; वेक्टर वैक्टर के लिए ऑर्थोगोनल, और निर्देशित किया जाता है ताकि आधार का सही अभिविन्यास हो:

हम हड्डियों द्वारा परिभाषा का विश्लेषण करते हैं, बहुत सारी दिलचस्प बातें हैं!

तो, हम निम्नलिखित महत्वपूर्ण बिंदुओं को उजागर कर सकते हैं:

1) स्रोत सदिश , परिभाषा के अनुसार, लाल तीरों द्वारा दर्शाया गया है संरेख नहीं. संरेख सदिशों के मामले पर थोड़ी देर बाद विचार करना उचित होगा।

2) वैक्टर लिए गए सख्त क्रम में: – "ए" को "बी" से गुणा किया जाता है, "हो" से "ए" नहीं। सदिश गुणन का परिणाम VECTOR है, जिसे नीले रंग से दर्शाया गया है। यदि सदिशों को उल्टे क्रम में गुणा किया जाता है, तो हमें लम्बाई में बराबर और दिशा में विपरीत (लाल रंग) सदिश मिलता है। यानी समता .

3) आइए अब सदिश गुणनफल के ज्यामितीय अर्थ से परिचित हों। यह एक बहुत महत्वपूर्ण मुद्दा है! नीले वेक्टर की लंबाई (और, इसलिए, क्रिमसन वेक्टर) संख्यात्मक रूप से वैक्टर पर बने समांतर चतुर्भुज के क्षेत्रफल के बराबर है। चित्र में, इस समांतर चतुर्भुज को काले रंग से छायांकित किया गया है।

टिप्पणी : ड्राइंग योजनाबद्ध है, और निश्चित रूप से, क्रॉस उत्पाद की नाममात्र लंबाई समानांतर चतुर्भुज के क्षेत्र के बराबर नहीं है।

हमें एक याद है ज्यामितीय सूत्र: एक समांतर चतुर्भुज का क्षेत्रफल आसन्न भुजाओं के गुणनफल और उनके बीच के कोण की ज्या के बराबर होता है. इसलिए, पूर्वगामी के आधार पर, वेक्टर उत्पाद की लंबाई की गणना करने का सूत्र मान्य है:

मैं इस बात पर जोर देता हूं कि सूत्र में हम वेक्टर की लंबाई के बारे में बात कर रहे हैं, न कि वेक्टर के बारे में। व्यावहारिक अर्थ क्या है? और अर्थ ऐसा है कि विश्लेषणात्मक ज्यामिति की समस्याओं में, एक समांतर चतुर्भुज का क्षेत्र अक्सर एक सदिश उत्पाद की अवधारणा के माध्यम से पाया जाता है:

हमें दूसरा महत्वपूर्ण सूत्र मिलता है। समांतर चतुर्भुज (लाल बिंदीदार रेखा) का विकर्ण इसे दो समान त्रिभुजों में विभाजित करता है। इसलिए, वैक्टर (लाल छायांकन) पर निर्मित त्रिभुज का क्षेत्रफल सूत्र द्वारा पाया जा सकता है:

4) एक समान रूप से महत्वपूर्ण तथ्य यह है कि सदिश सदिशों के लिए ओर्थोगोनल है, अर्थात . बेशक, विपरीत रूप से निर्देशित वेक्टर (क्रिमसन एरो) भी मूल वैक्टर के लिए ऑर्थोगोनल है।

5) वेक्टर को निर्देशित किया जाता है ताकि आधारयह है सहीअभिविन्यास। के बारे में एक पाठ में एक नए आधार पर संक्रमणके बारे में विस्तार से बता चुका हूं विमान अभिविन्यास, और अब हम यह पता लगाएंगे कि अंतरिक्ष का अभिविन्यास क्या है। मैं आपकी उंगलियों पर समझाऊंगा दांया हाथ . मानसिक रूप से गठबंधन करें तर्जनी अंगुली वेक्टर के साथ और बीच की ऊँगलीवेक्टर के साथ। रिंग फिंगरऔर छोटी उंगलीअपनी हथेली में दबाएं। नतीजतन अँगूठा - वेक्टर उत्पाद दिखेगा। यह सही-उन्मुख आधार है (यह चित्र में है)। अब सदिशों की अदला-बदली करें ( सूचकांक और बीच की उंगलियां ) कुछ स्थानों पर, अंगूठा घूम जाएगा, और वेक्टर उत्पाद पहले से ही नीचे दिखेगा। यह भी एक दक्षिणपंथी आधार है। शायद आपके पास एक प्रश्न है: वामपंथी अभिविन्यास किस आधार पर है? "असाइन करें" एक ही उंगलियां बायां हाथ vectors , और बायाँ आधार और बायाँ स्थान अभिविन्यास प्राप्त करें (इस स्थिति में, अंगूठा निचले सदिश की दिशा में स्थित होगा). आलंकारिक रूप से बोलते हुए, ये आधार अलग-अलग दिशाओं में "मोड़" या उन्मुख स्थान हैं। और इस अवधारणा को कुछ दूर की कौड़ी या अमूर्त नहीं माना जाना चाहिए - उदाहरण के लिए, सबसे साधारण दर्पण अंतरिक्ष के उन्मुखीकरण को बदलता है, और यदि आप "प्रतिबिंबित वस्तु को दर्पण से बाहर खींचते हैं", तो सामान्य तौर पर यह संभव नहीं होगा इसे "मूल" के साथ मिलाएं। वैसे, तीन अंगुलियों को दर्पण में लाएं और प्रतिबिंब का विश्लेषण करें ;-)

... यह कितना अच्छा है कि अब आप इसके बारे में जान गए हैं दाएं और बाएं उन्मुखआधार, क्योंकि अभिविन्यास परिवर्तन के बारे में कुछ व्याख्याताओं के बयान भयानक हैं =)

संरेख सदिशों का सदिश उत्पाद

परिभाषा पर विस्तार से काम किया गया है, यह पता लगाना बाकी है कि जब वैक्टर संरेख होते हैं तो क्या होता है। यदि सदिश समतल हैं, तो उन्हें एक सीधी रेखा पर रखा जा सकता है और हमारा समांतर चतुर्भुज भी एक सीधी रेखा में "गुना" होता है। ऐसा क्षेत्र, जैसा कि गणितज्ञ कहते हैं, पतितसमानांतर चतुर्भुज शून्य है। सूत्र से भी यही होता है - शून्य या 180 डिग्री की ज्या शून्य के बराबर होती है, जिसका अर्थ है कि क्षेत्रफल शून्य है

इस प्रकार, यदि, तब . सख्ती से बोलना, क्रॉस उत्पाद स्वयं शून्य वेक्टर के बराबर है, लेकिन व्यवहार में इसे अक्सर उपेक्षित किया जाता है और लिखा जाता है कि यह केवल शून्य के बराबर है।

विशेष मामलाएक वेक्टर और स्वयं का क्रॉस उत्पाद है:

क्रॉस उत्पाद का उपयोग करके, आप त्रि-आयामी वैक्टर की संपार्श्विकता की जांच कर सकते हैं, और हम इस समस्या का विश्लेषण भी करेंगे।

समाधान के लिए व्यावहारिक उदाहरणशायद जरूरत पड़े त्रिकोणमितीय तालिकाइससे ज्या के मूल्यों का पता लगाने के लिए।

खैर, आग लगाओ:

उदाहरण 1

ए) वैक्टर के वेक्टर उत्पाद की लंबाई पाएं यदि

ख) सदिशों पर निर्मित समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए यदि

समाधान: नहीं, यह कोई टाइपो नहीं है, मैंने जानबूझकर प्रारंभिक डेटा को स्थिति में समान बनाया है। क्योंकि समाधानों का डिज़ाइन अलग होगा!

a) स्थिति के अनुसार, इसे खोजना आवश्यक है लंबाईवेक्टर (वेक्टर उत्पाद)। संबंधित सूत्र के अनुसार:

उत्तर:

चूंकि यह लंबाई के बारे में पूछा गया था, तो उत्तर में हम आयाम - इकाइयों का संकेत देते हैं।

b) स्थिति के अनुसार, इसे खोजना आवश्यक है वर्गवैक्टर पर निर्मित समांतर चतुर्भुज। इस समांतर चतुर्भुज का क्षेत्रफल संख्यात्मक रूप से क्रॉस उत्पाद की लंबाई के बराबर है:

उत्तर:

कृपया ध्यान दें कि वेक्टर उत्पाद के उत्तर में कोई बात नहीं है, जिसके बारे में हमसे पूछा गया था आंकड़ा क्षेत्र, क्रमशः, आयाम वर्ग इकाई है।

हम हमेशा देखते हैं कि स्थिति के अनुसार क्या खोजना आवश्यक है, और इसके आधार पर, हम तैयार करते हैं साफ़उत्तर। यह शाब्दिक प्रतीत हो सकता है, लेकिन शिक्षकों के बीच पर्याप्त साहित्यकार हैं, और अच्छे अवसरों वाले कार्य को संशोधन के लिए वापस कर दिया जाएगा। यद्यपि यह विशेष रूप से तनावपूर्ण नाइटपिक नहीं है - यदि उत्तर गलत है, तो किसी को यह आभास हो जाता है कि व्यक्ति साधारण चीजों को नहीं समझता है और / या कार्य के सार को नहीं समझा है। किसी भी समस्या को हल करते हुए इस क्षण को हमेशा नियंत्रण में रखना चाहिए उच्च गणितऔर अन्य विषयों में भी।

बड़ा अक्षर "एन" कहाँ गया? सिद्धांत रूप में, यह अतिरिक्त रूप से समाधान के लिए अटका हो सकता है, लेकिन रिकॉर्ड को छोटा करने के लिए, मैंने नहीं किया। मुझे आशा है कि हर कोई इसे समझता है और एक ही चीज़ का पदनाम है।

के लिए एक लोकप्रिय उदाहरण है स्वतंत्र समाधान:

उदाहरण 2

यदि सदिशों पर बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए

वेक्टर उत्पाद के माध्यम से त्रिभुज का क्षेत्रफल ज्ञात करने का सूत्र टिप्पणियों में परिभाषा में दिया गया है। पाठ के अंत में समाधान और उत्तर।

व्यवहार में, कार्य वास्तव में बहुत सामान्य है, त्रिभुजों को आमतौर पर प्रताड़ित किया जा सकता है।

अन्य समस्याओं को हल करने के लिए, हमें चाहिए:

वैक्टर के क्रॉस उत्पाद के गुण

हमने वेक्टर उत्पाद के कुछ गुणों पर पहले ही विचार कर लिया है, हालाँकि, मैं उन्हें इस सूची में शामिल करूँगा।

मनमाना वैक्टर और मनमाना संख्या के लिए, निम्नलिखित गुण:

1) जानकारी के अन्य स्रोतों में, यह आइटम आमतौर पर गुणों में प्रतिष्ठित नहीं है, लेकिन यह व्यावहारिक रूप से बहुत महत्वपूर्ण है। तो रहने दो।

2) - संपत्ति की भी चर्चा ऊपर की गई है, कभी-कभी इसे कहा जाता है anticommutativity. दूसरे शब्दों में, सदिशों का क्रम मायने रखता है।

3) - संयोजन या जोड़नेवालावेक्टर उत्पाद कानून। सदिश उत्पाद की सीमा से स्थिरांक आसानी से निकाल लिए जाते हैं। वास्तव में, वे वहाँ क्या कर रहे हैं?

4) - वितरण या वितरणवेक्टर उत्पाद कानून। कोष्ठक खोलने में भी कोई समस्या नहीं है।

एक प्रदर्शन के रूप में, एक संक्षिप्त उदाहरण पर विचार करें:

उदाहरण 3

अगर खोजो

समाधान:शर्त के अनुसार, सदिश उत्पाद की लंबाई का पता लगाना फिर से आवश्यक है। आइए हमारे लघुचित्र को पेंट करें:

(1) साहचर्य कानूनों के अनुसार, हम वेक्टर उत्पाद की सीमा से परे स्थिरांक निकालते हैं।

(2) हम मॉड्यूल से स्थिरांक निकालते हैं, जबकि मॉड्यूल माइनस साइन को "खा" देता है। लंबाई ऋणात्मक नहीं हो सकती।

(3) जो आगे है वह स्पष्ट है।

उत्तर:

आग पर लकड़ी फेंकने का समय आ गया है:

उदाहरण 4

सदिशों पर निर्मित त्रिभुज के क्षेत्रफल की गणना करें यदि

समाधान: सूत्र की सहायता से त्रिभुज का क्षेत्रफल ज्ञात कीजिए . रोड़ा यह है कि वैक्टर "सीई" और "टी" स्वयं वैक्टर के योग के रूप में दर्शाए जाते हैं। यहाँ एल्गोरिथ्म मानक है और कुछ हद तक पाठ के उदाहरण संख्या 3 और 4 की याद दिलाता है। वैक्टर का डॉट उत्पाद. आइए इसे स्पष्टता के लिए तीन चरणों में विभाजित करें:

1) पहले चरण में, हम वेक्टर उत्पाद को वेक्टर उत्पाद के माध्यम से व्यक्त करते हैं, वास्तव में, वेक्टर को वेक्टर के संदर्भ में व्यक्त करें. लंबाई पर अभी तक कोई शब्द नहीं!

(1) हम सदिशों के व्यंजकों को प्रतिस्थापित करते हैं।

(2) वितरणात्मक नियमों का प्रयोग करते हुए, बहुपदों के गुणन के नियम के अनुसार कोष्ठक खोलिए।

(3) साहचर्य कानूनों का उपयोग करते हुए, हम वेक्टर उत्पादों से परे सभी स्थिरांक निकालते हैं। थोड़े से अनुभव के साथ, क्रियाएं 2 और 3 एक साथ की जा सकती हैं।

(4) सुखद संपत्ति के कारण पहला और अंतिम पद शून्य (शून्य वेक्टर) के बराबर है। दूसरे कार्यकाल में, हम सदिश उत्पाद के एंटीकॉम्यूटिविटी गुण का उपयोग करते हैं:

(5) हम समान शब्द प्रस्तुत करते हैं।

नतीजतन, वेक्टर एक वेक्टर के माध्यम से व्यक्त किया गया, जिसे प्राप्त करने की आवश्यकता थी:

2) दूसरे चरण में, हमें आवश्यक वेक्टर उत्पाद की लंबाई का पता चलता है। यह क्रिया उदाहरण 3 के समान है:

3) अभीष्ट त्रिभुज का क्षेत्रफल ज्ञात कीजिए:

समाधान के चरण 2-3 को एक पंक्ति में व्यवस्थित किया जा सकता है।

उत्तर:

माना समस्या परीक्षणों में काफी आम है, यहाँ एक स्वतंत्र समाधान के लिए एक उदाहरण है:

उदाहरण 5

अगर खोजो

पाठ के अंत में संक्षिप्त समाधान और उत्तर। आइए देखें कि पिछले उदाहरणों का अध्ययन करते समय आप कितने चौकस थे ;-)

निर्देशांक में वैक्टर का क्रॉस उत्पाद

, ऑर्थोनॉर्मल आधार पर दिया गया है, सूत्र द्वारा व्यक्त किया गया है:

सूत्र वास्तव में सरल है: हम निर्धारक की शीर्ष पंक्ति में निर्देशांक वैक्टर लिखते हैं, हम दूसरी और तीसरी पंक्तियों में वैक्टर के निर्देशांक को "पैक" करते हैं, और हम डालते हैं सख्त क्रम में- पहले, वेक्टर "ve" के निर्देशांक, फिर वेक्टर "डबल-ve" के निर्देशांक। यदि वैक्टर को एक अलग क्रम में गुणा करने की आवश्यकता है, तो लाइनों की अदला-बदली भी की जानी चाहिए:

उदाहरण 10

जांचें कि क्या निम्नलिखित अंतरिक्ष वैक्टर संरेख हैं:
ए)
बी)

समाधान: परीक्षण इस पाठ में दिए गए कथनों में से एक पर आधारित है: यदि सदिश समरेख हैं, तो उनका क्रॉस उत्पाद शून्य (शून्य सदिश) है: .

ए) वेक्टर उत्पाद खोजें:

इसलिए सदिश समरेख नहीं हैं।

बी) वेक्टर उत्पाद खोजें:

उत्तर: ए) समरेख नहीं, बी)

यहाँ, शायद, सदिशों के सदिश गुणनफल के बारे में सभी बुनियादी जानकारी है।

यह खंड बहुत बड़ा नहीं होगा, क्योंकि कुछ समस्याएँ हैं जहाँ सदिशों के मिश्रित उत्पाद का उपयोग किया जाता है। वास्तव में, सब कुछ परिभाषा, ज्यामितीय अर्थ और कुछ कामकाजी सूत्रों पर आधारित होगा।

सदिशों का मिश्रित उत्पाद तीन सदिशों का गुणनफल होता है:

इस तरह वे एक ट्रेन की तरह खड़े होते हैं और प्रतीक्षा करते हैं, जब तक उनकी गणना नहीं हो जाती तब तक वे प्रतीक्षा नहीं कर सकते।

पहले फिर से परिभाषा और चित्र:

परिभाषा: मिश्रित उत्पाद गैर समतलीयवैक्टर, इस क्रम में लिया, कहा जाता है समांतर चतुर्भुज की मात्रा, इन सदिशों पर निर्मित, यदि आधार सही है तो "+" चिह्न और आधार छोड़े जाने पर "-" चिन्ह से सुसज्जित है।

चलो ड्राइंग करते हैं। हमारे लिए अदृश्य रेखाएँ बिंदीदार रेखा द्वारा खींची जाती हैं:

आइए परिभाषा में गोता लगाएँ:

2) वैक्टर लिए गए एक निश्चित क्रम में, अर्थात्, उत्पाद में वैक्टर का क्रमचय, जैसा कि आप अनुमान लगा सकते हैं, परिणाम के बिना नहीं जाता है।

3) ज्यामितीय अर्थ पर टिप्पणी करने से पहले, मैं स्पष्ट तथ्य पर ध्यान दूंगा: सदिशों का मिश्रित गुणनफल एक NUMBER है: . शैक्षिक साहित्य में, डिजाइन कुछ अलग हो सकता है, मैं एक मिश्रित उत्पाद को नामित करता था, और "पे" अक्षर के साथ गणना का परिणाम।

ए-प्राथमिकता मिश्रित उत्पाद समांतर चतुर्भुज का आयतन है, वैक्टर पर निर्मित (आकृति लाल वैक्टर और काली रेखाओं के साथ खींची गई है)। अर्थात्, संख्या दिए गए समांतर चतुर्भुज के आयतन के बराबर है।

टिप्पणी : आरेखण योजनाबद्ध है।

4) आइए फिर से आधार और स्थान के उन्मुखीकरण की अवधारणा से परेशान न हों। अंतिम भाग का अर्थ यह है कि वॉल्यूम में माइनस साइन जोड़ा जा सकता है। सरल शब्दों में, मिश्रित उत्पाद नकारात्मक हो सकता है: .

सदिशों पर बने समांतर चतुर्भुज के आयतन की गणना करने का सूत्र सीधे परिभाषा से अनुसरण करता है।

7.1। क्रॉस उत्पाद की परिभाषा

तीन गैर समतलीय सदिश a , b और c , संकेतित क्रम में लिए गए हैं, एक सम त्रिक बनाते हैं यदि तीसरे सदिश c के अंत से पहले सदिश a से दूसरे सदिश b तक का सबसे छोटा मोड़ वामावर्त देखा जाता है, और एक बाईं ओर अगर दक्षिणावर्त (चित्र देखें। 16)।

वेक्टर ए और वेक्टर बी के वेक्टर उत्पाद को वेक्टर सी कहा जाता है, जो:

1. वेक्टर ए और बी के लंबवत, यानी सी ^ ए और सी ^ बी;

2. इसकी लंबाई संख्यात्मक रूप से वैक्टर ए और पर निर्मित समानांतर चतुर्भुज के क्षेत्र के बराबर हैबीपक्षों के रूप में (अंजीर देखें। 17), यानी।

3. सदिश a , b और c एक सम त्रिक बनाते हैं।

सदिश गुणनफल को a x b या [a,b] निरूपित किया जाता है। एक वेक्टर उत्पाद की परिभाषा से, orts के बीच निम्नलिखित संबंध मैं सीधे अनुसरण करता हूं, जेऔर क(अंजीर देखें। 18):

आई एक्स जे \u003d के, जे एक्स के \u003d आई, के एक्स आई \u003d जे।
आइए सिद्ध करें, उदाहरण के लिए, किमैं एक्सजे \u003d के।

1) के ^ आई, के ^ जे;

2) |के |=1, लेकिन | मैं एक्स जे| = |मैं | |जे| पाप (90°)=1;

3) सदिश i , j और कएक सम त्रिक बनाएँ (चित्र 16 देखें)।

7.2। क्रॉस उत्पाद गुण

1. जब कारकों को पुनर्व्यवस्थित किया जाता है, तो सदिश गुणन चिह्न बदल जाता है, अर्थात और xb \u003d (b xa) (चित्र 19 देखें)।

वैक्टर a xb और b xa समरेख हैं, समान मॉड्यूल हैं (समानांतर चतुर्भुज का क्षेत्र अपरिवर्तित रहता है), लेकिन विपरीत दिशा में निर्देशित होते हैं (ट्रिपल a, b, a xb और a, b, b x a विपरीत अभिविन्यास के)। वह है axb = -(bxa).

2. वेक्टर उत्पाद में एक स्केलर कारक के संबंध में एक संयोजन गुण होता है, अर्थात l (a xb) \u003d (l a) x b \u003d a x (l b)।

चलो एल> 0। सदिश l (a xb) सदिशों a और b के लंबवत है। वेक्टर ( एलए) एक्स बीसदिशों a और के लंबवत भी है बी(वैक्टर ए, एललेकिन एक ही विमान में लेट जाओ)। तो वैक्टर एल(एक एक्सबी) और ( एलए) एक्स बीसंरेख। यह स्पष्ट है कि उनकी दिशाएँ मेल खाती हैं। उनकी लंबाई समान है:

इसीलिए एल(एक एक्सबी) = एलएक एक्सबी। के लिए भी यही सिद्ध होता है एल<0.

3. दो शून्येतर सदिश a और बीसंरेख हैं यदि और केवल यदि उनका सदिश गुणनफल शून्य सदिश के बराबर है, अर्थात, और ||b<=>और xb \u003d 0।

विशेष रूप से, i *i =j *j =k *k =0 ।

4. वेक्टर उत्पाद में वितरण गुण होता है:

(क+ख)एक्सएस = ए एक्सएस + बी xs।

बिना प्रमाण के स्वीकार करो।

7.3। निर्देशांक के संदर्भ में क्रॉस उत्पाद अभिव्यक्ति

हम वेक्टर क्रॉस उत्पाद तालिका i का उपयोग करेंगे, जेऔर कश्मीर:

यदि पहले वेक्टर से दूसरे तक के सबसे छोटे पथ की दिशा तीर की दिशा से मेल खाती है, तो उत्पाद तीसरे वेक्टर के बराबर होता है, यदि यह मेल नहीं खाता है, तो तीसरा वेक्टर माइनस साइन के साथ लिया जाता है।

माना दो सदिश a =a x i + a y जे+az कऔर बी = बीएक्स मैं+ द्वारा जे+बज़ क. आइए इन वैक्टरों के वेक्टर उत्पाद को बहुपद के रूप में गुणा करके (वेक्टर उत्पाद के गुणों के अनुसार) खोजें:

परिणामी सूत्र को और भी छोटा लिखा जा सकता है:

चूंकि समानता का दाहिना पक्ष (7.1) पहली पंक्ति के तत्वों के संदर्भ में तीसरे क्रम के निर्धारक के विस्तार से मेल खाता है। समानता (7.2) को याद रखना आसान है।

7.4। क्रॉस उत्पाद के कुछ अनुप्रयोग

सदिशों की संरेखता स्थापित करना

एक समांतर चतुर्भुज और एक त्रिभुज का क्षेत्रफल ज्ञात करना

वैक्टर के क्रॉस उत्पाद की परिभाषा के अनुसार एऔर बी |ए एक्सबी | =|ए | * |b |sin g , यानी S par = |a x b |. और, इसलिए, डी एस \u003d 1/2 | ए एक्स बी |।

एक बिंदु के बारे में बल के क्षण का निर्धारण

मान लीजिए बिंदु A पर एक बल लगता है एफ = एबीजाने देना के बारे में- अंतरिक्ष में कुछ बिंदु (चित्र 20 देखें)।

भौतिकी से ज्ञात होता है कि टॉर्कः एफ बिंदु के सापेक्ष के बारे मेंवेक्टर कहा जाता है एम ,जो बिंदु से होकर गुजरता है के बारे मेंऔर:

1) बिंदुओं से गुजरने वाले समतल के लंबवत ओ, ए, बी;

2) संख्यात्मक रूप से बल और भुजा के गुणनफल के बराबर

3) सदिश OA और A B के साथ एक सम त्रिक बनाता है।

इसलिए, एम \u003d ओए एक्स एफ।

रोटेशन की रैखिक गति ढूँढना

रफ़्तार विएक कोणीय वेग से घूमते हुए कठोर शरीर का बिंदु M डब्ल्यूएक निश्चित अक्ष के चारों ओर, यूलर सूत्र v \u003d w x r द्वारा निर्धारित किया जाता है, जहाँ r \u003d OM, जहाँ O अक्ष का कुछ निश्चित बिंदु है (चित्र 21 देखें)।

Yandex.RTB R-A-339285-1

एक सदिश उत्पाद की अवधारणा देने से पहले, आइए हम त्रि-आयामी अंतरिक्ष में सदिशों के क्रमित ट्रिपल a → , b → , c → के उन्मुखीकरण के प्रश्न की ओर मुड़ें।

आरंभ करने के लिए, सदिशों a → , b → , c → को एक बिंदु से अलग रखें। सदिश c → की दिशा के आधार पर ट्रिपल a → , b → , c → का अभिविन्यास दाएँ या बाएँ है। सदिश a → से b → सदिश c → के अंत से जिस दिशा में सबसे छोटा मोड़ बनाया गया है, उससे त्रिगुण a → , b → , c → का रूप निर्धारित किया जाएगा।

यदि सबसे छोटा घुमाव वामावर्त है, तो सदिशों का त्रिक a → , b → , c → कहलाता है सहीयदि दक्षिणावर्त - बाएं.

इसके बाद, दो असंरेख सदिश a → और b → लें। आइए फिर सदिशों A B → = a → और A C → = b → को बिंदु A से स्थगित करें। आइए एक सदिश A D → = c → का निर्माण करें, जो A B → और AC → दोनों के साथ-साथ लंबवत है। इस प्रकार, सदिश A D → = c → का निर्माण करते समय, हम इसे एक दिशा या विपरीत दिशा देकर दो काम कर सकते हैं (चित्रण देखें)।

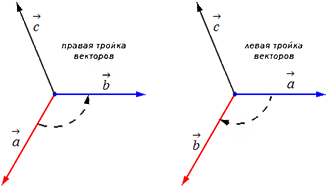
सदिशों की क्रमित तिकड़ी a → , b → , c → हो सकती है, जैसा कि हमें पता चला है, सदिश की दिशा के आधार पर दाएं या बाएं।

ऊपर से, हम वेक्टर उत्पाद की परिभाषा पेश कर सकते हैं। यह परिभाषा त्रि-आयामी अंतरिक्ष के एक आयताकार समन्वय प्रणाली में परिभाषित दो वैक्टरों के लिए दी गई है।

परिभाषा 1

दो सदिशों a → और b → का सदिश गुणनफल हम त्रि-आयामी अंतरिक्ष के एक आयताकार समन्वय प्रणाली में दिए गए ऐसे वेक्टर को कॉल करेंगे जैसे कि:

• यदि सदिश a → और b → संरेख हैं, तो यह शून्य होगा;
• यह सदिश a →​​ और सदिश b → दोनों के लंबवत होगा। ∠ a → c → = ∠ b → c → = π 2 ;
• इसकी लंबाई सूत्र द्वारा निर्धारित की जाती है: c → = a → b → sin ∠ a → , b → ;
• सदिशों के त्रिक a → , b → , c → का वही अभिविन्यास है जो दिए गए निर्देशांक तंत्र का है।

सदिशों a → और b → के अनुप्रस्थ गुणनफल में निम्नलिखित चिह्न हैं: a → × b → ।

क्रॉस उत्पाद निर्देशांक

चूंकि किसी भी वेक्टर के निर्देशांक प्रणाली में कुछ निर्देशांक होते हैं, इसलिए वेक्टर उत्पाद की दूसरी परिभाषा प्रस्तुत करना संभव है, जो आपको वैक्टर के दिए गए निर्देशांक से इसके निर्देशांक खोजने की अनुमति देगा।

परिभाषा 2

त्रि-आयामी अंतरिक्ष के एक आयताकार समन्वय प्रणाली में दो सदिशों का सदिश गुणनफल a → = (a x; a y; a z) और b → = (b x; b y; b z) सदिश को कॉल करें c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , जहाँ i → , j → , k → निर्देशांक सदिश हैं।

वेक्टर उत्पाद को तीसरे क्रम के एक वर्ग मैट्रिक्स के निर्धारक के रूप में दर्शाया जा सकता है, जहां पहली पंक्ति ओर्टा वैक्टर i → , j → , k → है, दूसरी पंक्ति में वेक्टर a → के निर्देशांक होते हैं, और तीसरा सदिश b के निर्देशांक हैं → दिए गए आयताकार समन्वय प्रणाली में, यह मैट्रिक्स निर्धारक इस तरह दिखता है: c → = a → × b → = i → j → k → a x a y a z b x b y b z

पहली पंक्ति के तत्वों पर इस निर्धारक का विस्तार करते हुए, हम समानता प्राप्त करते हैं: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b y k → = = a → × b → = ( a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

क्रॉस उत्पाद गुण

यह ज्ञात है कि निर्देशांक में वेक्टर उत्पाद को मैट्रिक्स c → = a → × b → = i → j → k → a x a y a z b x b y b z के निर्धारक के रूप में दर्शाया गया है, फिर आधार पर मैट्रिक्स निर्धारक गुणनिम्नलिखित वेक्टर उत्पाद गुण:

1. एंटीकम्यूटेटिविटी ए → × बी → = - बी → × ए →;
2. वितरण a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → या a → × b (1) → + b (2) → = a → × बी (1) → + ए → × बी (2) → ;
3. साहचर्य λ a → × b → = λ a → × b → या a → × (λ b →) = λ a → × b → , जहाँ λ एक स्वेच्छ वास्तविक संख्या है।

इन गुणों के जटिल प्रमाण नहीं हैं।

उदाहरण के लिए, हम एक सदिश उत्पाद के प्रतिक्रमणीयता गुण को सिद्ध कर सकते हैं।

एंटीकम्यूटेटिविटी का प्रमाण

परिभाषा के अनुसार, a → × b → = i → j → k → a x a y a z b x b y b z और b → × a → = i → j → k → b x b y b z a x a y a z । और यदि मैट्रिक्स की दो पंक्तियों को आपस में बदल दिया जाता है, तो मैट्रिक्स के निर्धारक का मान विपरीत में बदल जाना चाहिए, इसलिए, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , जो सदिश उत्पाद की प्रतिक्रमणीयता को सिद्ध करता है।

वेक्टर उत्पाद - उदाहरण और समाधान

ज्यादातर मामलों में, तीन प्रकार के कार्य होते हैं।

पहले प्रकार की समस्याओं में, दो सदिशों की लंबाई और उनके बीच का कोण आमतौर पर दिया जाता है, लेकिन आपको क्रॉस उत्पाद की लंबाई का पता लगाने की आवश्यकता है। इस स्थिति में, निम्न सूत्र c → = a → b → sin ∠ a → , b → का उपयोग करें।

उदाहरण 1

वैक्टर a → और b → के क्रॉस उत्पाद की लंबाई ज्ञात करें यदि a → = 3 , b → = 5 , ∠ a → , b → = π 4 ज्ञात है।

समाधान

वैक्टर a → और b → के वेक्टर उत्पाद की लंबाई की परिभाषा का उपयोग करते हुए, हम इस समस्या को हल करते हैं: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

उत्तर: 15 2 2 .

दूसरे प्रकार के कार्यों का वैक्टर के निर्देशांक के साथ संबंध होता है, उनमें एक वेक्टर उत्पाद, उसकी लंबाई आदि शामिल होते हैं। दिए गए सदिशों के ज्ञात निर्देशांकों के माध्यम से खोजे जाते हैं ए → = (ए एक्स; ए वाई; ए जेड) और बी → = (बी एक्स; बी वाई; बी जेड) .

इस प्रकार के कार्य के लिए, आप कार्यों के बहुत सारे विकल्प हल कर सकते हैं। उदाहरण के लिए, वैक्टर a → और b → के निर्देशांक नहीं, बल्कि फॉर्म के निर्देशांक वैक्टर में उनका विस्तार b → = b x i → + b y j → + b z k → और c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , या सदिश a → और b → उनके निर्देशांक द्वारा दिए जा सकते हैं प्रारंभ और अंत बिंदु।

निम्नलिखित उदाहरणों पर विचार करें।

उदाहरण 2

एक आयताकार समन्वय प्रणाली में दो वैक्टर सेट होते हैं a → = (2; 1; - 3), b → = (0; - 1; 1)। उनका सदिश गुणनफल ज्ञात कीजिए।

समाधान

दूसरी परिभाषा के अनुसार, हम दिए गए निर्देशांक में दो वैक्टरों का वेक्टर उत्पाद पाते हैं: a → × b → = (a y b z - a z b y) i → + (az b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 कश्मीर → .

यदि हम मैट्रिक्स निर्धारक के माध्यम से वेक्टर उत्पाद लिखते हैं, तो इस उदाहरण का समाधान इस प्रकार है: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

उत्तर: a → × b → = - 2 i → - 2 j → - 2 k → .

उदाहरण 3

वैक्टर i → - j → और i → + j → + k → , जहाँ i → , j → , k → - एक आयताकार कार्तीय निर्देशांक प्रणाली के orts के क्रॉस उत्पाद की लंबाई ज्ञात करें।

समाधान

सबसे पहले, आइए दिए गए आयताकार समन्वय प्रणाली में दिए गए वेक्टर उत्पाद i → - j → × i → + j → + k → के निर्देशांक खोजें।

यह ज्ञात है कि सदिश i → - j → और i → + j → + k → के निर्देशांक क्रमशः (1; - 1; 0) और (1; 1; 1) हैं। मैट्रिक्स निर्धारक का उपयोग करके वेक्टर उत्पाद की लंबाई पाएं, फिर हमारे पास i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → है + 2 क → .

इसलिए, वेक्टर उत्पाद i → - j → × i → + j → + k → दिए गए समन्वय प्रणाली में निर्देशांक (- 1; - 1; 2) है।

हम सूत्र द्वारा वेक्टर उत्पाद की लंबाई पाते हैं (वेक्टर की लंबाई खोजने पर अनुभाग देखें): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

उत्तर: i → - j → × i → + j → + k → = 6। .

उदाहरण 4

तीन बिन्दुओं A (1 , 0 , 1) , B (0 , 2 , 3) ​​​​, C (1 , 4 , 2) के निर्देशांक एक आयताकार कार्तीय निर्देशांक प्रणाली में दिए गए हैं। एक ही समय में A B → और AC → के लिए लंबवत कुछ सदिश ज्ञात कीजिए।

समाधान

सदिश A B → और A C → के निर्देशांक क्रमशः (- 1; 2; 2) और (0; 4; 1) हैं। सदिशों A B → और A C → का सदिश गुणनफल प्राप्त करने के बाद, यह स्पष्ट है कि परिभाषा के अनुसार यह A B → और A C → दोनों के लिए लंबवत सदिश है, अर्थात यह हमारी समस्या का समाधान है। इसे A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → ज्ञात कीजिए।

उत्तर: - 6 i → + j → - 4 k → . लम्बवत सदिशों में से एक है।

वैक्टर के वेक्टर उत्पाद के गुणों का उपयोग करने पर तीसरे प्रकार की समस्याएं केंद्रित हैं। जिसे लगाने के बाद हमें दी गई समस्या का समाधान मिल जाएगा।

उदाहरण 5

सदिश a → और b → लंबवत हैं और उनकी लंबाई क्रमशः 3 और 4 है। क्रॉस उत्पाद की लंबाई पाएं 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

समाधान

सदिश गुणनफल के वितरण गुण से हम लिख सकते हैं 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

सहयोगीता की संपत्ति से, हम अंतिम अभिव्यक्ति में वेक्टर उत्पादों के संकेत से परे संख्यात्मक गुणांक निकालते हैं: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

वेक्टर उत्पाद a → × a → और b → × b → 0 के बराबर हैं, क्योंकि a → × a → = a → a → sin 0 = 0 और b → × b → = b → b → sin 0 = 0, फिर 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → । .

वेक्टर उत्पाद की एंटीकोमुटेटिविटी से यह निम्नानुसार है - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → । .

वेक्टर उत्पाद के गुणों का उपयोग करते हुए, हम समानता 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → प्राप्त करते हैं।

शर्त के अनुसार, सदिश a → और b → लंबवत हैं, अर्थात, उनके बीच का कोण π 2 के बराबर है। अब यह केवल पाए गए मानों को संबंधित सूत्रों में बदलने के लिए बना हुआ है: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60।

उत्तर: 3 ए → - बी → × ए → - 2 बी → = 60।

परिभाषा के अनुसार वैक्टर के क्रॉस उत्पाद की लंबाई a → × b → = a → · b → · sin ∠ a → , b → है। चूँकि यह पहले से ही ज्ञात है (स्कूल के पाठ्यक्रम से) कि एक त्रिभुज का क्षेत्रफल उसके दो भुजाओं की लंबाई के आधे उत्पाद के बराबर होता है, जो इन भुजाओं के बीच के कोण की ज्या से गुणा होता है। इसलिए, वेक्टर उत्पाद की लंबाई एक समांतर चतुर्भुज के क्षेत्र के बराबर है - एक दोगुना त्रिकोण, अर्थात्, वैक्टर के रूप में पक्षों का उत्पाद a → और b → , एक बिंदु से, साइन द्वारा निर्धारित उनके बीच के कोण sin ∠ a → , b → .

यह वेक्टर उत्पाद का ज्यामितीय अर्थ है।

वेक्टर उत्पाद का भौतिक अर्थ

यांत्रिकी में, भौतिकी की शाखाओं में से एक, वेक्टर उत्पाद के लिए धन्यवाद, आप अंतरिक्ष में एक बिंदु के सापेक्ष बल का क्षण निर्धारित कर सकते हैं।

परिभाषा 3

बल के क्षण के तहत F →, बिंदु B पर लागू, बिंदु A के सापेक्ष हम निम्नलिखित वेक्टर उत्पाद A B → × F → को समझेंगे।

यदि आप टेक्स्ट में कोई गलती देखते हैं, तो कृपया इसे हाइलाइट करें और Ctrl+Enter दबाएं

इकाई वेक्टर- यह वेक्टर, जिसका निरपेक्ष मान (मापांक) एक के बराबर है। इकाई वेक्टर को निरूपित करने के लिए, हम सबस्क्रिप्ट ई का उपयोग करेंगे। इसलिए, यदि एक वेक्टर दिया गया है ए, तो इसका इकाई वेक्टर वेक्टर होगा एई. यह इकाई वेक्टर उसी दिशा में इंगित करता है जिस दिशा में स्वयं वेक्टर होता है ए, और इसका मापांक एक के बराबर है, अर्थात एक ई \u003d 1।

ज़ाहिर तौर से, ए= ए एई (अ - वेक्टर मापांक ए). यह उस नियम से अनुसरण करता है जिसके द्वारा एक वेक्टर द्वारा एक स्केलर को गुणा करने का कार्य किया जाता है।

यूनिट वैक्टरअक्सर समन्वय प्रणाली के समन्वय अक्षों से जुड़ा होता है (विशेष रूप से, कार्टेशियन समन्वय प्रणाली के अक्षों के साथ)। इनमें से दिशा वैक्टरसंबंधित अक्षों की दिशाओं के साथ मेल खाता है, और उनकी उत्पत्ति अक्सर समन्वय प्रणाली की उत्पत्ति के साथ मिलती है।

मैं आपको वह याद दिला दूं कार्तीय समन्वय प्रणालीअंतरिक्ष में पारंपरिक रूप से एक बिंदु पर परस्पर लंबवत कुल्हाड़ियों का तिगुना कहा जाता है जिसे मूल कहा जाता है। समन्वय अक्षों को आमतौर पर अक्षर X, Y, Z द्वारा निरूपित किया जाता है और क्रमशः भुज अक्ष, समन्वय अक्ष और अनुप्रयुक्त अक्ष कहा जाता है। डेसकार्टेस ने स्वयं केवल एक अक्ष का उपयोग किया था, जिस पर भुज प्लॉट किए गए थे। उपयोग की योग्यता प्रणालीकुल्हाड़ी उसके छात्रों की है। इसलिए मुहावरा कार्तीय समन्वय प्रणालीऐतिहासिक रूप से गलत। बेहतर बात आयताकार निर्देशांक तरीकाया ऑर्थोगोनल समन्वय प्रणाली. फिर भी, हम परंपराओं को नहीं बदलेंगे और भविष्य में हम यह मानेंगे कि कार्टेशियन और आयताकार (ऑर्थोगोनल) समन्वय प्रणाली एक ही हैं।

इकाई वेक्टर, एक्स अक्ष के साथ निर्देशित, निरूपित है मैं, इकाई वेक्टर, Y अक्ष के साथ निर्देशित, निरूपित है जे, ए इकाई वेक्टर, Z अक्ष के साथ निर्देशित, निरूपित है क. वैक्टर मैं, जे, कबुलाया orts(चित्र 12, बाएं), उनके पास एकल मॉड्यूल हैं, अर्थात
मैं = 1, जे = 1, के = 1।

कुल्हाड़ियों और orts आयताकार समन्वय प्रणालीकुछ मामलों में उनके अन्य नाम और पद होते हैं। तो, भुज अक्ष X को स्पर्शरेखा अक्ष कहा जा सकता है, और इसकी इकाई वेक्टर को निरूपित किया जाता है τ (ग्रीक छोटा अक्षर ताऊ), y- अक्ष सामान्य अक्ष है, इसकी इकाई सदिश को निरूपित किया जाता है एन, अनुप्रयुक्त अक्ष द्विसामान्य का अक्ष है, इसकी इकाई सदिश को निरूपित किया जाता है बी. यदि सार वही रहता है तो नाम क्यों बदलते हैं?

तथ्य यह है कि, उदाहरण के लिए, यांत्रिकी में, निकायों की गति का अध्ययन करते समय, आयताकार समन्वय प्रणाली का अक्सर उपयोग किया जाता है। इसलिए, यदि समन्वय प्रणाली स्वयं गतिहीन है, और एक गतिमान वस्तु के निर्देशांक में परिवर्तन को इस गतिहीन प्रणाली में ट्रैक किया जाता है, तो आमतौर पर अक्ष X, Y, Z और उनके को दर्शाते हैं ortsक्रमश: मैं, जे, क.

लेकिन अक्सर, जब कोई वस्तु किसी प्रकार के घुमावदार प्रक्षेपवक्र (उदाहरण के लिए, एक वृत्त के साथ) के साथ चलती है, तो इस वस्तु के साथ चलने वाली समन्वय प्रणाली में यांत्रिक प्रक्रियाओं पर विचार करना अधिक सुविधाजनक होता है। यह इस तरह के गतिशील समन्वय प्रणाली के लिए है कि कुल्हाड़ियों और उनके इकाई वैक्टर के अन्य नामों का उपयोग किया जाता है। यह अभी स्वीकार किया गया है। इस मामले में, एक्स-अक्ष को उस बिंदु पर प्रक्षेपवक्र के लिए स्पर्शिक रूप से निर्देशित किया जाता है जहां यह वस्तु वर्तमान में स्थित है। और फिर इस अक्ष को अब एक्स अक्ष नहीं कहा जाता है, लेकिन स्पर्शरेखा अक्ष, और इसकी इकाई वेक्टर को अब निरूपित नहीं किया जाता है मैं, ए τ . Y अक्ष को प्रक्षेपवक्र की वक्रता की त्रिज्या के साथ निर्देशित किया जाता है (एक वृत्त में गति के मामले में - वृत्त के केंद्र तक)। और चूंकि त्रिज्या स्पर्शरेखा के लंबवत है, अक्ष को सामान्य की धुरी कहा जाता है (लंबवत और सामान्य समान हैं)। इस अक्ष के ओर्ट को अब निरूपित नहीं किया जाता है जे, ए एन. तीसरी धुरी (पूर्व Z) पिछले दो के लंबवत है। यह एक सदिश के साथ एक असामान्य है बी(चित्र 12, दाएं)। वैसे, इस मामले में आयताकार समन्वय प्रणालीअक्सर "प्राकृतिक" या प्राकृतिक के रूप में जाना जाता है।