विचरण विकल्पों के वर्गों के अंकगणितीय माध्य के योग के बराबर होता है। यादृच्छिक चर के विचरण की गणना कैसे करें

हालाँकि, यह विशेषता अकेले अध्ययन करने के लिए पर्याप्त नहीं है अनियमित चर. दो निशानेबाजों की कल्पना करें जो एक लक्ष्य पर शूटिंग कर रहे हैं। एक सटीक रूप से शूट करता है और केंद्र के करीब हिट करता है, और दूसरा ... केवल मज़े करना और लक्ष्य बनाना भी नहीं। लेकिन मजे की बात यह है कि औसतपरिणाम बिल्कुल पहले शूटर जैसा ही होगा! यह स्थिति सशर्त रूप से निम्नलिखित यादृच्छिक चर द्वारा सचित्र है:

"स्नाइपर" गणितीय अपेक्षा के बराबर है, हालांकि, "दिलचस्प व्यक्ति" के लिए: - यह भी शून्य है!

इस प्रकार, यह निर्धारित करने की आवश्यकता है कि कितनी दूर छितरा हुआलक्ष्य के केंद्र के सापेक्ष गोलियां (यादृच्छिक मान) ( गणितीय अपेक्षा) ठीक और बिखरनेलैटिन से केवल के रूप में अनुवादित फैलाव .

आइए देखें कि पाठ के पहले भाग के उदाहरणों में से एक में यह संख्यात्मक विशेषता कैसे निर्धारित की जाती है:

वहां हमें इस खेल की निराशाजनक गणितीय अपेक्षा मिली, और अब हमें इसके विचरण की गणना करनी है, जो लक्षितके माध्यम से ।

आइए जानें कि औसत मूल्य के सापेक्ष जीत/हार कितनी दूर "बिखरे हुए" हैं। जाहिर है, इसके लिए हमें गणना करने की आवश्यकता है मतभेदके बीच एक यादृच्छिक चर के मूल्यऔर उसकी गणितीय अपेक्षा:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

अब परिणामों का योग करना आवश्यक प्रतीत होता है, लेकिन यह तरीका अच्छा नहीं है - इस कारण से कि बाईं ओर के दोलन एक दूसरे को दाईं ओर के दोलनों के साथ रद्द कर देंगे। तो, उदाहरण के लिए, "शौकिया" शूटर (उपरोक्त उदाहरण)मतभेद हो जाएगा , और जब जोड़ा जाएगा तो वे शून्य देंगे, इसलिए हमें उसकी शूटिंग के बिखरने का कोई अनुमान नहीं मिलेगा।

इस झुंझलाहट को दूर करने के लिए, विचार करें मॉड्यूलमतभेद, लेकिन तकनीकी कारणजब वे चुकता हो जाते हैं तो दृष्टिकोण ने जड़ें जमा ली हैं। तालिका में समाधान की व्यवस्था करना अधिक सुविधाजनक है:

और यहाँ यह गणना करने के लिए भीख माँगता है भारित औसतवर्ग विचलन का मान। यह क्या है? यह उनका है अपेक्षित मूल्य, जो बिखरने का उपाय है:

– परिभाषाफैलाव। परिभाषा से यह तुरंत स्पष्ट हो जाता है कि विचरण ऋणात्मक नहीं हो सकता- अभ्यास के लिए ध्यान दें!

आइए याद रखें कि अपेक्षा कैसे प्राप्त करें। चुकता अंतरों को संबंधित संभावनाओं से गुणा करें (तालिका निरंतरता):
- लाक्षणिक रूप से बोलना, यह "कर्षण बल" है,
और परिणामों को सारांशित करें:

क्या आपको नहीं लगता कि जीत की पृष्ठभूमि में परिणाम बहुत बड़ा निकला? यह सही है - हम वर्ग कर रहे थे, और अपने खेल के आयाम पर लौटने के लिए, हमें वर्गमूल लेने की आवश्यकता है। इस मान को कहा जाता है मानक विचलन और ग्रीक अक्षर "सिग्मा" द्वारा दर्शाया गया है:

कभी-कभी इस अर्थ को कहा जाता है मानक विचलन .

इसका अर्थ क्या है? यदि हम गणितीय अपेक्षा से बाईं ओर और दाईं ओर माध्य से विचलन करते हैं मानक विचलन:

- तो इस अंतराल पर यादृच्छिक चर के सबसे संभावित मान "केंद्रित" होंगे। हम वास्तव में क्या देख रहे हैं:

हालांकि, ऐसा हुआ कि बिखरने के विश्लेषण में लगभग हमेशा फैलाव की अवधारणा के साथ काम करते हैं। आइए देखें कि खेलों के संबंध में इसका क्या अर्थ है। यदि निशानेबाजों के मामले में हम लक्ष्य के केंद्र के सापेक्ष हिट की "सटीकता" के बारे में बात कर रहे हैं, तो यहां फैलाव दो चीजों की विशेषता है:

सबसे पहले, यह स्पष्ट है कि जैसे-जैसे दरें बढ़ती हैं, विचरण भी बढ़ता है। इसलिए, उदाहरण के लिए, यदि हम 10 गुना वृद्धि करते हैं, तो गणितीय अपेक्षा 10 गुना बढ़ जाएगी, और विचरण 100 गुना बढ़ जाएगा (जैसे ही यह एक द्विघात मान होता है). लेकिन ध्यान दें कि खेल के नियम नहीं बदले हैं! केवल दरें बदल गई हैं, मोटे तौर पर बोलते हुए, हम 10 रूबल की शर्त लगाते थे, अब 100।

दूसरा, अधिक दिलचस्प बिंदु यह है कि विचरण खेल की शैली की विशेषता है। खेल दरों को मानसिक रूप से ठीक करें किसी निश्चित स्तर पर, और देखें कि यहाँ क्या है:

एक कम विचरण खेल एक सतर्क खेल है। खिलाड़ी सबसे विश्वसनीय योजनाओं का चयन करता है, जहां वह एक समय में बहुत अधिक नहीं हारता/जीतता है। उदाहरण के लिए, रूले में लाल/काली प्रणाली (लेख का उदाहरण 4 देखें यादृच्छिक चर) .

उच्च विचरण खेल। उसे अक्सर कहा जाता है फैलावखेल। यह खेल की एक साहसिक या आक्रामक शैली है जहां खिलाड़ी "एड्रेनालाईन" योजनाओं को चुनता है। चलो कम से कम याद करते हैं "मार्टिंगेल", जिसमें दांव पर लगी रकम पिछले पैराग्राफ के "शांत" खेल से अधिक परिमाण के आदेश हैं।

पोकर में स्थिति सांकेतिक है: तथाकथित हैं तंगजो खिलाड़ी सतर्क रहते हैं और अपने खेल कोष से "हिलाते" हैं (बैंकरोल). आश्चर्य नहीं कि उनके बैंकरोल में ज्यादा उतार-चढ़ाव नहीं होता (कम विचरण)। इसके विपरीत, यदि किसी खिलाड़ी का विचरण अधिक है, तो वह आक्रामक है। वह अक्सर जोखिम लेता है, बड़े दांव लगाता है और दोनों एक बड़े बैंक को तोड़ सकता है और टुकड़ों में जा सकता है।

विदेशी मुद्रा में भी यही होता है, और इसी तरह - बहुत सारे उदाहरण हैं।

इसके अलावा, सभी मामलों में इससे कोई फर्क नहीं पड़ता कि खेल एक पैसे के लिए है या हजारों डॉलर के लिए है। हर स्तर के अपने निम्न और उच्च विचरण वाले खिलाड़ी होते हैं। खैर, औसत जीत के लिए, जैसा कि हम याद करते हैं, "जिम्मेदार" अपेक्षित मूल्य.

आपने शायद ध्यान दिया होगा कि विचरण का पता लगाना एक लंबी और श्रमसाध्य प्रक्रिया है। लेकिन गणित उदार है:

प्रसरण ज्ञात करने का सूत्र

यह सूत्र सीधे विचरण की परिभाषा से लिया गया है, और हम इसे तुरंत प्रचलन में लाते हैं। मैं ऊपर से हमारे खेल के साथ प्लेट की नकल करूंगा:

और मिली उम्मीद।

हम दूसरे तरीके से विचरण की गणना करते हैं। सबसे पहले, आइए गणितीय अपेक्षा खोजें - यादृच्छिक चर का वर्ग। द्वारा गणितीय अपेक्षा की परिभाषा:

इस मामले में:

इस प्रकार, सूत्र के अनुसार:

जैसा कि वे कहते हैं, अंतर महसूस करें। और व्यवहार में, निश्चित रूप से, सूत्र को लागू करना बेहतर है (जब तक कि शर्त की आवश्यकता न हो)।

हम हल करने और डिजाइन करने की तकनीक में महारत हासिल करते हैं:

उदाहरण 6

इसकी गणितीय अपेक्षा, प्रसरण और मानक विचलन ज्ञात कीजिए।

यह कार्य हर जगह पाया जाता है, और, एक नियम के रूप में, सार्थक अर्थ के बिना चला जाता है।
आप संख्या के साथ कई प्रकाश बल्बों की कल्पना कर सकते हैं जो कुछ संभावनाओं के साथ पागलखाने में प्रकाश करते हैं :)

समाधान: तालिका में मुख्य गणनाओं को संक्षेप में प्रस्तुत करना सुविधाजनक है। सबसे पहले, हम प्रारंभिक डेटा को शीर्ष दो पंक्तियों में लिखते हैं। फिर हम उत्पादों की गणना करते हैं, फिर और अंत में सही कॉलम में रकम:

दरअसल, लगभग सब कुछ तैयार है। तीसरी पंक्ति में, एक तैयार गणितीय अपेक्षा तैयार की गई थी: .

फैलाव की गणना सूत्र द्वारा की जाती है:

और अंत में, मानक विचलन:
- व्यक्तिगत रूप से, मैं आमतौर पर 2 दशमलव स्थानों तक घूमता हूं।

सभी गणना एक कैलकुलेटर पर की जा सकती है, और इससे भी बेहतर - एक्सेल में:

यहां गलत होना मुश्किल है :)

उत्तर:

जो चाहते हैं वे अपने जीवन को और भी सरल बना सकते हैं और मेरा लाभ उठा सकते हैं कैलकुलेटर (प्रदर्शन), जो न केवल इस समस्या को तुरंत हल करता है, बल्कि निर्माण भी करता है विषयगत ग्राफिक्स (जल्दी आना). कार्यक्रम कर सकते हैं पुस्तकालय में डाउनलोड करें- यदि आपने कम से कम एक अध्ययन सामग्री डाउनलोड की है, या प्राप्त करते हैं एक और तरीका. परियोजना का समर्थन करने के लिए धन्यवाद!

कार्यों की एक जोड़ी स्वतंत्र समाधान:

उदाहरण 7

परिभाषा के अनुसार पिछले उदाहरण के यादृच्छिक चर के प्रसरण की गणना करें।

और एक समान उदाहरण:

उदाहरण 8

एक असतत यादृच्छिक चर अपने स्वयं के वितरण कानून द्वारा दिया जाता है:

हां, यादृच्छिक चर के मान काफी बड़े हो सकते हैं (से उदाहरण असली काम) , और यहां, यदि संभव हो तो, एक्सेल का उपयोग करें। वैसे, उदाहरण 7 में - यह तेज़, अधिक विश्वसनीय और अधिक सुखद है।

समाधान और उत्तर पृष्ठ के निचले भाग में।

पाठ के दूसरे भाग के समापन में, हम एक और विशिष्ट कार्य का विश्लेषण करेंगे, कोई एक छोटा सा रिबास भी कह सकता है:

उदाहरण 9

एक असतत यादृच्छिक चर केवल दो मान ले सकता है: और , तथा । संभाव्यता, गणितीय अपेक्षा और विचरण ज्ञात हैं।

समाधान: आइए अज्ञात संभावना से शुरू करते हैं। चूंकि एक यादृच्छिक चर केवल दो मान ले सकता है, तो संबंधित घटनाओं की संभावनाओं का योग:

और तब से ।

यह खोजना बाकी है ..., कहना आसान है :) लेकिन ओह ठीक है, यह शुरू हो गया। गणितीय अपेक्षा की परिभाषा के अनुसार:
- ज्ञात मानों को प्रतिस्थापित करें:

- और इस समीकरण से और कुछ नहीं निकाला जा सकता है, सिवाय इसके कि आप इसे सामान्य दिशा में फिर से लिख सकते हैं:

या:

आगे की कार्रवाइयों के बारे में, मुझे लगता है कि आप अनुमान लगा सकते हैं। आइए सिस्टम बनाएं और हल करें:

दशमलव- यह, ज़ाहिर है, एक पूर्ण अपमान है; दोनों समीकरणों को 10 से गुणा करें:

और 2 से विभाजित करें:

यह ज़्यादा बेहतर है। पहले समीकरण से हम व्यक्त करते हैं:
(यह आसान तरीका है)- दूसरे समीकरण में स्थानापन्न करें:

हम निर्माण कर रहे हैं वर्गऔर सरलीकरण करें:

हम इससे गुणा करते हैं:

नतीजतन, द्विघात समीकरण, इसका विभेदक ज्ञात कीजिए:
- उत्तम!

और हमें दो समाधान मिलते हैं:

1) अगर , फिर ;

2) अगर , फिर ।

मूल्यों की पहली जोड़ी शर्त को संतुष्ट करती है। उच्च संभावना के साथ, सब कुछ सही है, लेकिन, फिर भी, हम वितरण कानून लिखते हैं:

और एक जाँच करें, अर्थात्, अपेक्षा का पता लगाएं:

यदि अध्ययन के तहत जनसंख्या को समूहों में विभाजित किया जाता है, तो इस जनसंख्या के लिए निम्नलिखित प्रकार के फैलाव की गणना की जा सकती है: कुल, समूह (इंट्राग्रुप), समूह औसत (इंट्राग्रुप का औसत), इंटरग्रुप।

प्रारंभ में, यह निर्धारण के गुणांक की गणना करता है, जो दर्शाता है कि अध्ययन किए गए गुण की कुल भिन्नता का कौन सा हिस्सा अंतरसमूह भिन्नता है, यानी। समूहीकरण के कारण:

अनुभवजन्य सहसंबंध अनुपात समूहीकरण (तथ्यात्मक) और प्रभावी संकेतों के बीच संबंध की जकड़न की विशेषता है।

अनुभवजन्य सहसंबंध अनुपात 0 से 1 तक मान ले सकता है।

अनुभवजन्य सहसंबंध अनुपात के आधार पर रिश्ते की निकटता का आकलन करने के लिए, आप चाडॉक संबंधों का उपयोग कर सकते हैं:

उदाहरण 4डिजाइन और सर्वेक्षण संगठनों द्वारा काम के प्रदर्शन पर निम्नलिखित आंकड़े हैं: अलगआकारसंपत्ति:

परिभाषित करना:

1) कुल विचरण;

2) समूह फैलाव;

3) समूह फैलाव का औसत;

4) इंटरग्रुप फैलाव;

5) प्रसरण जोड़ने के नियम पर आधारित कुल प्रसरण;

6) निर्धारण और अनुभवजन्य सहसंबंध का गुणांक।

अपने निष्कर्ष निकालें।

समाधान:

1. आइए स्वामित्व के दो रूपों के उद्यमों द्वारा किए गए कार्य की औसत मात्रा निर्धारित करें:

कुल विचरण की गणना करें:

2. समूह औसत परिभाषित करें:

मिलियन रूबल;

एमएलएन रगड़।

समूह भिन्नताएं:

;

3. समूह प्रसरणों के औसत की गणना करें:

4. अंतरसमूह विचरण का निर्धारण करें:

5. प्रसरण जोड़ने के नियम के आधार पर कुल प्रसरण की गणना करें:

6. निर्धारण का गुणांक निर्धारित करें:

.

इस प्रकार, डिजाइन और सर्वेक्षण संगठनों द्वारा किए गए कार्य की मात्रा 22% उद्यमों के स्वामित्व के रूप पर निर्भर करती है।

अनुभवजन्य सहसंबंध अनुपात की गणना सूत्र द्वारा की जाती है

.

परिकलित संकेतक का मूल्य इंगित करता है कि उद्यम के स्वामित्व के रूप में काम की मात्रा की निर्भरता कम है।

उदाहरण 5उत्पादन स्थलों के तकनीकी अनुशासन के सर्वेक्षण के परिणामस्वरूप, निम्नलिखित आंकड़े प्राप्त हुए:

निर्धारण का गुणांक निर्धारित करें

.

इसके विपरीत, if एक गैर-ऋणात्मक है a.e. एक ऐसा समारोह , तो इस पर एक बिल्कुल निरंतर संभाव्यता माप है जो कि इसका घनत्व है।

Lebesgue अभिन्न में माप का परिवर्तन:

,

संभाव्यता माप के संबंध में कोई बोरेल फ़ंक्शन कहां है।

फैलाव, प्रकार और फैलाव के गुण फैलाव की अवधारणा

आंकड़ों में फैलावअंकगणित माध्य से वर्गित विशेषता के व्यक्तिगत मूल्यों के मानक विचलन के रूप में पाया जाता है। प्रारंभिक डेटा के आधार पर, यह सरल और भारित विचरण सूत्रों द्वारा निर्धारित किया जाता है:

1. सरल विचरण(अवर्गीकृत डेटा के लिए) की गणना सूत्र द्वारा की जाती है:

2. भारित विचरण (भिन्नता श्रृंखला के लिए):

जहां n - आवृत्ति (दोहराव कारक X)

विचरण खोजने का एक उदाहरण

यह पृष्ठ विचरण को खोजने के एक मानक उदाहरण का वर्णन करता है, आप इसे खोजने के लिए अन्य कार्यों को भी देख सकते हैं

उदाहरण 1. समूह का निर्धारण, समूह का औसत, समूह के बीच और कुल विचरण

उदाहरण 2. एक समूहन तालिका में प्रसरण और विचरण का गुणांक ज्ञात करना

उदाहरण 3. असतत श्रेणी में प्रसरण ज्ञात करना

उदाहरण 4. हमारे पास 20 छात्रों के समूह के लिए निम्नलिखित डेटा है पत्राचार विभाग. सुविधा वितरण की अंतराल श्रृंखला बनाना, सुविधा के औसत मूल्य की गणना करना और इसके विचरण का अध्ययन करना आवश्यक है

आइए एक अंतराल समूह बनाते हैं। आइए सूत्र द्वारा अंतराल की सीमा निर्धारित करें:

जहां एक्स मैक्स ग्रुपिंग फीचर का अधिकतम मूल्य है; X मिनट समूहीकरण सुविधा का न्यूनतम मान है; n अंतराल की संख्या है:

हम एन = 5 स्वीकार करते हैं। चरण है: ज \u003d (192 - 159) / 5 \u003d 6.6

आइए एक अंतराल समूह बनाते हैं

आगे की गणना के लिए, हम एक सहायक तालिका बनाएंगे:

X "i - अंतराल का मध्य। (उदाहरण के लिए, अंतराल के मध्य 159 - 165.6 \u003d 162.3)

छात्रों की औसत वृद्धि अंकगणितीय भारित औसत के सूत्र द्वारा निर्धारित की जाती है:

हम सूत्र द्वारा फैलाव निर्धारित करते हैं:

सूत्र को इस प्रकार परिवर्तित किया जा सकता है:

इस सूत्र से यह इस प्रकार है कि भिन्नता है विकल्पों के वर्गों के माध्य और वर्ग और माध्य के बीच का अंतर।

भिन्नता श्रृंखला में भिन्नताक्षणों की विधि के अनुसार समान अंतराल के साथ, फैलाव की दूसरी संपत्ति का उपयोग करके निम्नलिखित तरीके से गणना की जा सकती है (अंतराल के मूल्य से सभी विकल्पों को विभाजित करना)। विचरण की परिभाषा, क्षणों की विधि द्वारा गणना, निम्न सूत्र के अनुसार कम समय लगता है:

जहां i अंतराल का मान है; ए - सशर्त शून्य, जो उच्चतम आवृत्ति के साथ अंतराल के मध्य का उपयोग करने के लिए सुविधाजनक है; m1 पहले क्रम के क्षण का वर्ग है; एम 2 - दूसरे क्रम का क्षण

फ़ीचर विचरण (यदि सांख्यिकीय जनसंख्या में विशेषता इस तरह से बदलती है कि केवल दो परस्पर अनन्य विकल्प हैं, तो ऐसी परिवर्तनशीलता को वैकल्पिक कहा जाता है) की गणना सूत्र द्वारा की जा सकती है:

इस फैलाव सूत्र q = 1-p में प्रतिस्थापित करने पर, हम प्राप्त करते हैं:

फैलाव के प्रकार

कुल विचरणइस भिन्नता का कारण बनने वाले सभी कारकों के प्रभाव में संपूर्ण जनसंख्या पर एक विशेषता की भिन्नता को मापता है। यह कुल माध्य मान x से फीचर x के व्यक्तिगत मूल्यों के विचलन के माध्य वर्ग के बराबर है और इसे साधारण विचरण या भारित विचरण के रूप में परिभाषित किया जा सकता है।

इंट्राग्रुप विचरण यादृच्छिक भिन्नता की विशेषता है, अर्थात। भिन्नता का एक भाग, जो कारकों के लिए बेहिसाब प्रभाव के कारण होता है और समूह में अंतर्निहित विशेषता-कारक पर निर्भर नहीं करता है। ऐसा विचरण समूह के अंकगणितीय माध्य से X समूह के भीतर एक विशेषता के व्यक्तिगत मूल्यों के विचलन के माध्य वर्ग के बराबर है और इसकी गणना एक साधारण विचरण या भारित विचरण के रूप में की जा सकती है।

इस तरह, समूह के भीतर विचरण के उपायएक समूह के भीतर एक विशेषता की भिन्नता और सूत्र द्वारा निर्धारित की जाती है:

जहां xi - समूह औसत; नी समूह में इकाइयों की संख्या है।

उदाहरण के लिए, एक दुकान में श्रम उत्पादकता के स्तर पर श्रमिकों की योग्यता के प्रभाव का अध्ययन करने के कार्य में निर्धारित किए जाने वाले अंतर-समूह भिन्नताएं सभी संभावित कारकों (उपकरण की तकनीकी स्थिति) के कारण प्रत्येक समूह में उत्पादन में भिन्नता दिखाती हैं। उपकरणों और सामग्रियों की उपलब्धता, श्रमिकों की आयु, श्रम की तीव्रता, आदि), में अंतर को छोड़कर योग्यता श्रेणी(एक समूह के भीतर, सभी श्रमिकों की योग्यता समान होती है)।

समूह के भीतर भिन्नताओं का औसत यादृच्छिक भिन्नता को दर्शाता है, जो कि भिन्नता का वह हिस्सा है जो समूहीकरण कारक के अपवाद के साथ अन्य सभी कारकों के प्रभाव में हुआ है। इसकी गणना सूत्र द्वारा की जाती है:

इंटरग्रुप विचरणपरिणामी गुण की व्यवस्थित भिन्नता की विशेषता है, जो समूह में अंतर्निहित विशेषता-कारक के प्रभाव के कारण है। यह कुल माध्य से समूह के विचलन के माध्य वर्ग के बराबर है। इंटरग्रुप विचरण की गणना सूत्र द्वारा की जाती है:

समूहीकृत डेटा के लिए अवशिष्ट फैलाव- इंट्राग्रुप फैलाव का औसत:

जहाँ 2 j, j-वें समूह का अंतर-समूह प्रसरण है।

असमूहीकृत डेटा के लिए अवशिष्ट फैलावसन्निकटन सटीकता का एक उपाय है, अर्थात। मूल डेटा के लिए प्रतिगमन रेखा का सन्निकटन:
जहां y(t) प्रवृत्ति समीकरण के अनुसार पूर्वानुमान है; y t - गतिकी की प्रारंभिक श्रृंखला; n अंकों की संख्या है; p प्रतिगमन समीकरण (व्याख्यात्मक चर की संख्या) के गुणांकों की संख्या है।
इस उदाहरण में इसे कहा जाता है विचरण का निष्पक्ष अनुमान.

उदाहरण 1। टैरिफ श्रेणियों द्वारा एक संघ के तीन उद्यमों के श्रमिकों का वितरण निम्नलिखित आंकड़ों की विशेषता है:

टैरिफ श्रेणीकार्यरत	उद्यम में श्रमिकों की संख्या
	उद्यम 1	उद्यम 2	उद्यम 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

परिभाषित करना:
1. प्रत्येक उद्यम के लिए फैलाव (इंट्राग्रुप फैलाव);
2. इंट्राग्रुप फैलाव का औसत;
3. इंटरग्रुप फैलाव;
4. कुल विचरण।

समाधान।
समस्या को हल करने के लिए आगे बढ़ने से पहले, यह पता लगाना आवश्यक है कि कौन सी विशेषता प्रभावी है और कौन सी तथ्यात्मक है। विचाराधीन उदाहरण में, प्रभावी विशेषता "टैरिफ श्रेणी" है, और कारक विशेषता "उद्यम की संख्या (नाम)" है।
फिर हमारे पास तीन समूह (उद्यम) हैं जिनके लिए समूह औसत और इंट्राग्रुप भिन्नताओं की गणना करना आवश्यक है:

कंपनी	समूह औसत,	समूह के भीतर विचरण,
1	4	1,8

इंट्राग्रुप प्रसरणों का औसत ( अवशिष्ट फैलाव) सूत्र द्वारा परिकलित:

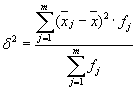
जहां आप गणना कर सकते हैं:
या:

फिर:
कुल फैलाव इसके बराबर होगा: s 2 \u003d 1.6 + 0 \u003d 1.6।
निम्नलिखित दो सूत्रों में से एक का उपयोग करके कुल विचरण की गणना भी की जा सकती है:

व्यावहारिक समस्याओं को हल करते समय, अक्सर एक संकेत से निपटना पड़ता है जो केवल दो वैकल्पिक मान लेता है। इस मामले में, वे किसी विशेषता के किसी विशेष मूल्य के वजन के बारे में बात नहीं कर रहे हैं, बल्कि कुल में इसके हिस्से के बारे में बात कर रहे हैं। यदि अध्ययन के तहत विशेषता वाली जनसंख्या इकाइयों के अनुपात को "द्वारा निरूपित किया जाता है" आर", और नहीं - के माध्यम से" क्यू”, तब फैलाव की गणना सूत्र द्वारा की जा सकती है:
एस 2 = पी × क्यू

उदाहरण # 2। ब्रिगेड के छह कर्मचारियों के आउटपुट के आंकड़ों के आधार पर, अंतरसमूह विचरण का निर्धारण करें और उनकी श्रम उत्पादकता पर कार्य शिफ्ट के प्रभाव का मूल्यांकन करें यदि कुल विचरण 12.2 है।

कार्यरत ब्रिगेड की संख्या	वर्किंग आउटपुट, पीसी।
	पहली पाली में	दूसरी पाली में
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

समाधान. प्रारंभिक आंकड़े

एक्स	f1	f2	च 3	f4	f5	f6	कुल
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
कुल	31	33	37	37	40	38

फिर हमारे पास 6 समूह हैं जिनके लिए समूह माध्य और इंट्राग्रुप प्रसरणों की गणना करना आवश्यक है।
1. प्रत्येक समूह का औसत मान ज्ञात कीजिए.







2. प्रत्येक समूह का माध्य वर्ग ज्ञात कीजिए.







हम एक तालिका में गणना के परिणामों को संक्षेप में प्रस्तुत करते हैं:

समूह संख्या	समूह औसत	इंट्राग्रुप विचरण
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. इंट्राग्रुप विचरणसमूह में अंतर्निहित कारक को छोड़कर, सभी कारकों के प्रभाव में समूह के भीतर अध्ययन (परिणामी) विशेषता के परिवर्तन (भिन्नता) की विशेषता है:
हम सूत्र का उपयोग करके इंट्राग्रुप फैलाव के औसत की गणना करते हैं:


4. इंटरग्रुप विचरणसमूह में अंतर्निहित एक कारक (तथ्यात्मक विशेषता) के प्रभाव में अध्ययन (परिणामस्वरूप) विशेषता के परिवर्तन (भिन्नता) की विशेषता है।
इंटरग्रुप फैलाव को इस प्रकार परिभाषित किया गया है:

कहाँ पे


फिर

कुल विचरणबिना किसी अपवाद के सभी कारकों (तथ्यात्मक लक्षण) के प्रभाव में अध्ययन (परिणामी) विशेषता के परिवर्तन (भिन्नता) की विशेषता है। समस्या की स्थिति से, यह 12.2 के बराबर है।
अनुभवजन्य सहसंबंध संबंधमापता है कि परिणामी विशेषता के कुल उतार-चढ़ाव का कितना हिस्सा अध्ययन किए गए कारक के कारण होता है। यह भाज्य विचरण का कुल विचरण का अनुपात है:

हम अनुभवजन्य सहसंबंध संबंध निर्धारित करते हैं:

सुविधाओं के बीच संबंध कमजोर या मजबूत (करीबी) हो सकते हैं। उनके मानदंड का मूल्यांकन चाडॉक पैमाने पर किया जाता है:
0.1 0.3 0.5 0.7 0.9 हमारे उदाहरण में, फीचर वाई फैक्टर एक्स के बीच संबंध कमजोर है
निर्धारण गुणांक।

आइए निर्धारण के गुणांक को परिभाषित करें:

इस प्रकार, 0.67% भिन्नता लक्षणों के बीच अंतर के कारण है, और 99.37% अन्य कारकों के कारण है।
निष्कर्ष: इस मामले में, श्रमिकों का उत्पादन एक विशेष पाली में काम पर निर्भर नहीं करता है, अर्थात। उनकी श्रम उत्पादकता पर कार्य शिफ्ट का प्रभाव महत्वपूर्ण नहीं है और अन्य कारकों के कारण है।

उदाहरण #3। औसत के आधार पर वेतनऔर श्रमिकों के दो समूहों के लिए इसके मूल्य से वर्ग विचलन, प्रसरणों को जोड़ने के लिए नियम लागू करके कुल विचरण ज्ञात कीजिए:

समाधान:
समूह के भीतर भिन्नताओं का औसत

इंटरग्रुप फैलाव को इस प्रकार परिभाषित किया गया है:


कुल विचरण होगा: 480 + 13824 = 14304

नमूना सर्वेक्षण के अनुसार, जमाकर्ताओं को शहर के सर्बैंक में जमा के आकार के अनुसार समूहीकृत किया गया था:

परिभाषित करना:

1) भिन्नता की सीमा;

2) औसत जमा राशि;

3) औसत रैखिक विचलन;

4) फैलाव;

5) मानक विचलन;

6) योगदान की भिन्नता का गुणांक।

समाधान:

इस वितरण श्रृंखला में खुले अंतराल हैं। ऐसी श्रृंखला में, पहले समूह के अंतराल का मान पारंपरिक रूप से अगले समूह के अंतराल के मान के बराबर माना जाता है, और अंतिम समूह के अंतराल का मान पिछले समूह के अंतराल के मान के बराबर होता है। एक।

दूसरे समूह का अंतराल मान 200 है, इसलिए, पहले समूह का मान भी 200 है। अंतिम समूह का अंतराल मान 200 है, जिसका अर्थ है कि अंतिम अंतराल का भी मान 200 के बराबर होगा।

1) भिन्नता की सीमा को सबसे बड़े और के बीच के अंतर के रूप में परिभाषित करें सबसे छोटा मानसंकेत:

योगदान के आकार में भिन्नता की सीमा 1000 रूबल है।

2) योगदान का औसत आकार अंकगणितीय भारित औसत के सूत्र द्वारा निर्धारित किया जाता है।

आइए प्रारंभिक रूप से परिभाषित करें असतत मात्राप्रत्येक अंतराल में विशेषता। ऐसा करने के लिए, सरल अंकगणितीय माध्य सूत्र का उपयोग करते हुए, हम अंतरालों के मध्य बिंदु पाते हैं।

पहले अंतराल का औसत मान इसके बराबर होगा:

दूसरा - 500, आदि।

आइए गणना के परिणामों को तालिका में रखें:

जमा राशि, रगड़।	योगदानकर्ताओं की संख्या, f	अंतराल के मध्य, x	एक्सएफ
200-400	32	300	9600
400-600	56	500	28000
600-800	120	700	84000
800-1000	104	900	93600
1000-1200	88	1100	96800
कुल	400	-	312000

शहर के Sberbank में औसत जमा 780 रूबल होगा:

3) औसत रैखिक विचलन कुल औसत से विशेषता के व्यक्तिगत मूल्यों के पूर्ण विचलन का अंकगणितीय औसत है:

अंतराल वितरण श्रृंखला में औसत रैखिक विचलन की गणना करने की प्रक्रिया इस प्रकार है:

1. अंकगणितीय भारित औसत की गणना की जाती है, जैसा कि पैराग्राफ 2 में दिखाया गया है)।

2. माध्य से भिन्न का पूर्ण विचलन निर्धारित किया जाता है:

3. प्राप्त विचलन को आवृत्तियों से गुणा किया जाता है:

4. संकेत को ध्यान में रखे बिना भारित विचलन का योग पाया जाता है:

5. भारित विचलन के योग को आवृत्तियों के योग से विभाजित किया जाता है:

गणना किए गए डेटा की तालिका का उपयोग करना सुविधाजनक है:

जमा राशि, रगड़।	योगदानकर्ताओं की संख्या, f	अंतराल के मध्य, x
200-400	32	300	-480	480	15360
400-600	56	500	-280	280	15680
600-800	120	700	-80	80	9600
800-1000	104	900	120	120	12480
1000-1200	88	1100	320	320	28160
कुल	400	-	-	-	81280

Sberbank ग्राहकों की जमा राशि का औसत रैखिक विचलन 203.2 रूबल है।

4) फैलाव अंकगणित माध्य से प्रत्येक विशेषता मान के वर्ग विचलन का अंकगणितीय माध्य है।

में फैलाव की गणना अंतराल श्रृंखलावितरण सूत्र के अनुसार किया जाता है:

इस मामले में विचरण की गणना करने की प्रक्रिया इस प्रकार है:

1. अंकगणितीय भारित औसत निर्धारित करें, जैसा कि पैराग्राफ 2 में दिखाया गया है)।

2. माध्य से विचलन ज्ञात कीजिए:

3. माध्य से प्रत्येक विकल्प के विचलन का वर्ग करना:

4. भार (आवृत्तियों) द्वारा वर्ग विचलन को गुणा करें:

5. प्राप्त कार्यों को सारांशित करें:

6. परिणामी राशि को भार (आवृत्तियों) के योग से विभाजित किया जाता है:

आइए गणनाओं को एक तालिका में रखें:

जमा राशि, रगड़।	योगदानकर्ताओं की संख्या, f	अंतराल के मध्य, x
200-400	32	300	-480	230400	7372800
400-600	56	500	-280	78400	4390400
600-800	120	700	-80	6400	768000
800-1000	104	900	120	14400	1497600
1000-1200	88	1100	320	102400	9011200
कुल	400	-	-	-	23040000