डमी के लिए ल'होपिटल का नियम: परिभाषा, समाधान उदाहरण, सूत्र। समाधान सीमा ऑनलाइन

समाधान ऑनलाइन कार्य सीमा. किसी बिंदु पर किसी फ़ंक्शन या कार्यात्मक अनुक्रम का सीमा मान ज्ञात करें, गणना करें सीमितअनंत पर फ़ंक्शन मान। एक संख्या श्रृंखला के अभिसरण को निर्धारित करें और बहुत कुछ किया जा सकता है धन्यवाद हमारे ऑनलाइन सेवा-। हम आपको फंक्शन लिमिट्स को ऑनलाइन जल्दी और सही तरीके से खोजने की अनुमति देते हैं। आप स्वयं फंक्शन वेरिएबल दर्ज करें और जिस सीमा तक वह चाहता है, हमारी सेवा आपके लिए सभी गणना करती है, एक सटीक और सरल उत्तर देती है। और के लिए ऑनलाइन सीमा ढूँढनाआप एक शाब्दिक अभिव्यक्ति में स्थिरांक वाले संख्यात्मक श्रृंखला और विश्लेषणात्मक फ़ंक्शन दोनों दर्ज कर सकते हैं। इस मामले में, पाया गया फ़ंक्शन सीमा में ये स्थिरांक अभिव्यक्ति में निरंतर तर्क के रूप में होंगे। हमारी सेवा खोजने की किसी भी जटिल समस्या का समाधान करती है सीमा ऑनलाइन, यह फ़ंक्शन और उस बिंदु को निर्दिष्ट करने के लिए पर्याप्त है जिस पर गणना करना आवश्यक है कार्य सीमा. कम्प्यूटिंग सीमा ऑनलाइन, आप उपयोग कर सकते हैं विभिन्न तरीकेऔर उनके समाधान के नियम, परिणाम की तुलना करते हुए समाधान ऑनलाइन सीमित करें www.site पर, जो कार्य के सफल समापन की ओर ले जाएगा - आप अपनी गलतियों और टाइपो से बचेंगे। या आप पूरी तरह से हम पर भरोसा कर सकते हैं और फ़ंक्शन सीमा की स्वतंत्र गणना पर अतिरिक्त प्रयास और समय खर्च किए बिना, अपने काम में हमारे परिणाम का उपयोग कर सकते हैं। हम अनंत जैसे सीमा मूल्यों के इनपुट की अनुमति देते हैं। आपको संख्यात्मक अनुक्रम का एक सामान्य शब्द दर्ज करना होगा और www.siteमूल्य की गणना करेगा ऑनलाइन सीमित करेंप्लस या माइनस अनंत तक।

गणितीय विश्लेषण की बुनियादी अवधारणाओं में से एक है कार्य सीमातथा अनुक्रम सीमाएक बिंदु पर और अनंत पर, सही ढंग से हल करने में सक्षम होना महत्वपूर्ण है सीमाएं. हमारी सेवा के साथ यह मुश्किल नहीं होगा। एक निर्णय किया जा रहा है सीमा ऑनलाइनसेकंड के भीतर, उत्तर सटीक और पूर्ण है। पथरी का अध्ययन शुरू होता है सीमा के लिए मार्ग, सीमाएंलगभग सभी वर्गों में उपयोग किया जाता है उच्च गणित, इसलिए हाथ में सर्वर होना उपयोगी है समाधान ऑनलाइन सीमित करेंजो साइट है।

L'Hopital का नियम (p. L.) कार्यों की सीमाओं की गणना की सुविधा प्रदान करता है। उदाहरण के लिए, आपको किसी फ़ंक्शन की सीमा ज्ञात करने की आवश्यकता है, जो कि शून्य की ओर झुकाव वाले फ़ंक्शन का अनुपात है। वे। फ़ंक्शन अनुपात अनिश्चितता 0/0 है। इसे खोलने में मदद मिलेगी। सीमा में, कार्यों के अनुपात को इन कार्यों के डेरिवेटिव के अनुपात से बदला जा सकता है। वे। अंश के व्युत्पन्न को हर के व्युत्पन्न से विभाजित करना और इस अंश से सीमा लेना आवश्यक है।

1. अनिश्चितता 0/0। प्रथम पी.एल.

अगर = 0, तो यदि बाद वाला मौजूद है।

2. फॉर्म की अनिश्चितता ∞/∞ सेकेंड पी. एल.

इस प्रकार की सीमा ज्ञात करना अनिश्चितताओं का प्रकटीकरण कहलाता है।

अगर = , तो अगर बाद वाला मौजूद है।

3. अनिश्चितताओं 0⋅∞, ∞-∞, 1 और 0 0 को परिवर्तन द्वारा अनिश्चितताओं 0/0 और ∞/∞ में घटाया जाता है। इस तरह की एक संकेतन सीमा का पता लगाते समय मामले को संक्षेप में इंगित करने का कार्य करती है। प्रत्येक अनिश्चितता अपने तरीके से प्रकट होती है। L'Hopital का नियम कई बार तब तक लागू किया जा सकता है जब तक हम अनिश्चितता से छुटकारा नहीं पा लेते। L'Hopital के नियम का अनुप्रयोग तब उपयोगी होता है जब डेरिवेटिव के अनुपात को कार्यों के अनुपात की तुलना में अधिक सुविधाजनक रूप में परिवर्तित किया जा सकता है।

• 0⋅∞ दो कार्यों का गुणनफल है, पहला शून्य की ओर जाता है, दूसरा अनंत तक;
• - अनंत की ओर प्रवृत्त कार्यों का अंतर;
• 1 डिग्री, इसका आधार एक और घातांक अनंत तक जाता है;
• ∞ 0 डिग्री, इसका आधार अनंत तक जाता है, और डिग्री शून्य हो जाती है;
• 0 0 डिग्री, इसका आधार 0 पर जाता है और घातांक भी शून्य हो जाता है।

उदाहरण 1. इस उदाहरण में, अनिश्चितता 0/0 . है

उदाहरण 2. यहाँ /∞

इन उदाहरणों में, हम अंश के अवकलज को हर के अवकलज से विभाजित करते हैं और x के लिए सीमित मान को प्रतिस्थापित करते हैं।

उदाहरण 3. अनिश्चितता का प्रकार 0⋅∞ .

हम अनिश्चितता 0⋅∞ को ∞/∞ में बदलते हैं, इसके लिए हम x को अंश 1/x के रूप में हर में स्थानांतरित करते हैं, अंश में हम अंश का व्युत्पन्न लिखते हैं, और हर में हर के व्युत्पन्न को लिखते हैं। .

उदाहरण 4 किसी फलन की सीमा ज्ञात कीजिए

यहाँ, रूप की अनिश्चितता 0 पहले हम फलन का लघुगणक लेते हैं, फिर उससे सीमा ज्ञात करते हैं

उत्तर पाने के लिए, आपको ई को -1 की शक्ति तक बढ़ाने की जरूरत है, हमें ई -1 मिलता है।

उदाहरण 5. यदि x → 0 . से सीमा की गणना करें

समाधान। अनिश्चितता प्रकार ∞ -∞ भिन्न को एक सामान्य हर में घटाकर, हम ∞-∞ से 0/0 तक जाते हैं। आइए L'Hospital के नियम को लागू करें, लेकिन फिर से हमें अनिश्चितता 0/0 मिलती है, इसलिए p. L. को दूसरी बार लागू किया जाना चाहिए। समाधान की तरह दिखता है:

= = = =
= =

उदाहरण 6 हल करें

समाधान। अनिश्चितता प्रकार ∞/∞, इसका विस्तार करने पर हमें मिलता है

मामलों में 3), 4), 5), फ़ंक्शन को पहले लॉगरिदमाइज़ किया जाता है और लॉगरिदम की सीमा पाई जाती है, और फिर वांछित सीमा ई को परिणामी शक्ति तक बढ़ा दिया जाता है।

उदाहरण 7 सीमा की गणना करें

समाधान। यहाँ अनिश्चितता का प्रकार 1 है। निरूपित ए =

फिर एलएनए = = = = 2.

लघुगणक का आधार ई है, इसलिए उत्तर प्राप्त करने के लिए आपको ई का वर्ग करना होगा, हमें ई 2 मिलता है।

कभी-कभी ऐसे मामले होते हैं जब डेरिवेटिव के संबंध के विपरीत कार्यों के संबंध की एक सीमा होती है, जो नहीं होती है।

एक उदाहरण पर विचार करें:

इसलिये sinx परिबद्ध है और x अनिश्चित काल तक बढ़ता है, दूसरा पद 0 है।

इस फ़ंक्शन की कोई सीमा नहीं है, क्योंकि यह 0 और 2 के बीच लगातार उतार-चढ़ाव करता है, पी। एल इस उदाहरण पर लागू नहीं होता है।

समय पर निर्देशांक की निर्भरता जब एक भौतिक बिंदु एक विमान में चलता है

मॉड्यूल गति निर्धारित करें (

A. समय से किसी भौतिक बिंदु के वेग का मापांक सूत्र द्वारा व्यक्त किया जाता है:

बी। । समय से भौतिक बिंदु के त्वरण का मॉड्यूल सूत्र द्वारा व्यक्त किया जाता है:

ये समीकरण निरंतर त्वरण के साथ एक भौतिक बिंदु की गति का वर्णन करते हैं

उपग्रह पृथ्वी के चारों ओर एक वृत्ताकार कक्षा में ऊँचाई पर चक्कर लगाता है

एक वृत्ताकार कक्षा में घूम रहा एक उपग्रह गुरुत्वाकर्षण बल के अधीन है

इस सूत्र को इस प्रकार सरल बनाया जा सकता है। शरीर के वजन पर

इस प्रकार, उपग्रह की रैखिक गति है

और कोणीय वेग

समस्या में मानी जाने वाली दोनों गेंदें एक बंद प्रणाली बनाती हैं, और एक लोचदार प्रभाव के मामले में, सिस्टम की गति और यांत्रिक (गतिज) ऊर्जा दोनों संरक्षित होती हैं। आइए हम दोनों संरक्षण कानूनों को लिखें (प्रभाव से पहले दूसरी गेंद की गतिहीनता को ध्यान में रखते हुए):

इस प्रकार, प्रभाव के परिणामस्वरूप घटना (पहली) गेंद ने अपनी गति को 1.05 मीटर/सेकेंड से 0.45 मीटर/सेकेंड तक कम कर दिया, हालांकि यह एक ही दिशा में आगे बढ़ना जारी रखा, और पहले स्थिर (दूसरी) गेंद ने बराबर गति हासिल की 1, 5 मी/से और अब दोनों गेंदें एक ही सीधी रेखा में और एक ही दिशा में चल रही हैं।

चूंकि गुब्बारे में गैस का द्रव्यमान बदलता है, गुब्बारे में गैस की प्रारंभिक और अंतिम अवस्थाओं को बॉयल-मैरियोट कानून या चार्ल्स कानून द्वारा संबंधित नहीं किया जा सकता है। यदि गुब्बारे में गैस बदलती है, तो प्रारंभिक और अंतिम गुब्बारे में गैस की अवस्थाओं को बॉयल-मैरियोट कानून द्वारा संबंधित नहीं किया जा सकता है। प्रत्येक राज्य मेंडेलीव-क्लैपेरॉन समीकरण लिखता है

लोपिटल नियम का उपयोग किए बिना किसी फ़ंक्शन की सीमा कैसे ज्ञात करें

सिस्टम संस्करण:
7.47 (16.04.2018)

सामान्य समाचार:
13.04.2018, 10:33

अन्तिम प्रश्न:
26.07.2018, 15:23

अंतिम उत्तर:
27.07.2018, 13:48

खंड गणित

बीजगणित, ज्यामिति, विश्लेषण, असतत गणित में परामर्श और समस्या समाधान।

इस खंड के सर्वश्रेष्ठ विशेषज्ञ

नमस्ते! मुझे इस प्रश्न में परेशानी हो रही है:

L'Hopital के नियम का उपयोग किए बिना किसी फलन की सीमा ज्ञात कीजिए

लिम (2x+3) [ ln (x+2) - ln x ] (लिम के नीचे लिखा है "x अनंत की ओर जाता है")

असाइनमेंट में सीमाओं के कई उदाहरण थे, लेकिन यह एक चकित करने वाला था। मुझे नहीं पता कि इसे कैसे हल किया जाए। हो सकता है कि किसी तरह दूसरी अद्भुत सीमा का उपयोग करें, लेकिन कैसे (केवल यही विचार दिमाग में आता है)?

मुझे बस उसी प्रश्न में पूछने दें कि क्या समस्या का ऐसा बयान होता है (यदि ऐसा होता है, तो मैं इसे बाद में भुगतान किए गए प्रश्न के रूप में पोस्ट करूंगा): फ़ंक्शन के लिए लैग्रेंज फॉर्म में टेलर फॉर्मूला को शेष अवधि के साथ लागू करना, गणना करना 0.001 की सटीकता के साथ मान; ए = 0.29।
यहाँ मुझे समझ में नहीं आता कि कौन सा कार्य? यह सेट नहीं है (?), कार्य ठीक वैसा ही लगता है जैसा मैंने इसे लिखा था। हो सकता है कि आप स्वयं समारोह ले सकते हैं, लेकिन कौन सा?

स्थिति: परामर्श बंद

हैलो अलेक्जेंड्रिब!
यह दूसरा है जिसे आपको उपयोग करने की आवश्यकता है! शुरू करने के लिए, आइए सरल करें:
लिम (2x+3) [ ln (x+2) - ln x ] = lim (2x+3) ln ((x+2)/x) = lim (2x+3) ln (1+2/x) = लिम ln ((1+2/x)^(2x+3)) = lim ln ((1+2/x)^2x)+lim ln ((1+2/x)^3) [दूसरी सीमा है शून्य , क्योंकि 2/x शून्य की ओर प्रवृत्त होता है और ln 1 = 0]
आइए परिवर्तन करें y = x/2, फिर lim ln ((1+2/x)^2x) = 4 lim ln ((1+1/y)^y) = 4 * ln e =4. उत्तर - 4।

कोई न कोई फंक्शन होना चाहिए।

संदेश भेजो
मॉडरेटर कर सकते हैं
केवल पोर्टल के सदस्य।
पोर्टल पर लॉगिन करें »
पंजीकरण "

ल'होपिटल का नियम: समाधान के सिद्धांत और उदाहरण

ल'होपिटल का नियम और अनिश्चितताओं का प्रकटीकरण

फॉर्म 0/0 या ∞/∞ की अनिश्चितताओं का प्रकटीकरण और कुछ अन्य अनिश्चितताएं जो दो इनफिनिटिमल या असीम रूप से बड़े कार्यों के अनुपात की सीमा की गणना करते समय उत्पन्न होती हैं, L'Hopital के नियम (वास्तव में दो नियम और उन पर टिप्पणी) का उपयोग करके बहुत सरल किया जाता है। )

सार एल अस्पताल के नियम यह है कि उस स्थिति में जब दो अपरिमित या अपरिमित रूप से बड़े फलनों के अनुपात की सीमा की गणना 0/0 या /∞ के रूप की अनिश्चितता देती है, दो फलनों के अनुपात की सीमा को उस सीमा से बदला जा सकता है उनके डेरिवेटिव का अनुपात और इस प्रकार, एक निश्चित परिणाम प्राप्त किया जा सकता है।

आइए, L'Hopital के नियमों के निरूपण की ओर बढ़ते हैं।

दो असीम रूप से छोटे मानों की सीमा के मामले के लिए L'Hopital का नियम. यदि कार्य एफ(एक्स) तथा जी(एक्स एक एक, और इस पड़ोस में जी‘(एक्स एकएक दूसरे के बराबर और शून्य के बराबर

(),

तो इन कार्यों के अनुपात की सीमा उनके डेरिवेटिव के अनुपात की सीमा के बराबर है

().

दो अपरिमित रूप से बड़ी मात्राओं की सीमा के मामले के लिए L'Hôpital का नियम. यदि कार्य एफ(एक्स) तथा जी(एक्स) बिंदु के कुछ पड़ोस में अवकलनीय हैं एक, बिंदु के संभावित अपवाद के साथ एक, और इस पड़ोस में जी‘(एक्स)≠0 और यदि और यदि x के रूप में इन कार्यों की सीमा बिंदु पर फ़ंक्शन के मान की ओर जाती है एकएक दूसरे के बराबर और अनंत के बराबर

(),

दूसरे शब्दों में, फॉर्म 0/0 या ∞/∞ की अनिश्चितताओं के लिए, दो कार्यों के अनुपात की सीमा उनके डेरिवेटिव के अनुपात की सीमा के बराबर है, यदि बाद वाला मौजूद है (परिमित या अनंत)।

टिप्पणियां.

1. L'Hopital के नियम तब भी लागू होते हैं जब फंक्शन एफ(एक्स) तथा जी(एक्स) पर परिभाषित नहीं हैं एक्स = एक.

2. यदि, फलनों के व्युत्पन्नों के अनुपात की सीमा की गणना करते समय एफ(एक्स) तथा जी(एक्स) हम फिर से फॉर्म 0/0 या ∞/∞ की अनिश्चितता में आते हैं, तो L'Hopital के नियमों को बार-बार (कम से कम दो बार) लागू किया जाना चाहिए।

3. L'Hopital के नियम तब भी लागू होते हैं जब फलनों (x) का तर्क एक अपरिमित संख्या की ओर प्रवृत्त होता है एक, और अनंत तक ( एक्स → ∞).

अन्य प्रकार की अनिश्चितताओं को भी 0/0 और /∞ प्रकार की अनिश्चितताओं में कम किया जा सकता है।

"शून्य से विभाजित शून्य" और "अनंत से विभाजित अनंत" प्रकारों की अनिश्चितताओं का प्रकटीकरण

उदाहरण 1

एक्स=2 फॉर्म 0/0 की अनिश्चितता की ओर ले जाता है। इसलिए, प्रत्येक फ़ंक्शन का व्युत्पन्न और हम प्राप्त करते हैं

अंश में, बहुपद के व्युत्पन्न की गणना की गई थी, और हर में, जटिल का व्युत्पन्न लॉगरिदमिक फ़ंक्शन. अंतिम बराबर चिह्न से पहले, सामान्य सीमा की गणना की गई थी, जिसमें x के बजाय एक ड्यूस रखा गया था।

उदाहरण 2 L'Hospital के नियम का उपयोग करके दो कार्यों के अनुपात की सीमा की गणना करें:

उदाहरण 3 L'Hospital के नियम का उपयोग करके दो कार्यों के अनुपात की सीमा की गणना करें:

समाधान। में प्रतिस्थापन दिया गया कार्यमूल्यों एक्स=0 फ़ॉर्म 0/0 की अनिश्चितता की ओर ले जाता है। इसलिए, हम अंश और हर में कार्यों के डेरिवेटिव की गणना करते हैं और प्राप्त करते हैं:

उदाहरण 4गणना

समाधान। किसी दिए गए फ़ंक्शन में x के बराबर प्लस अनंत के मान को प्रतिस्थापित करने से /∞ रूप की अनिश्चितता हो जाती है। इसलिए, हम L'Hopital का नियम लागू करते हैं:

टिप्पणी। आइए उन उदाहरणों पर चलते हैं जिनमें L'Hopital नियम को दो बार लागू करना पड़ता है, यानी दूसरे डेरिवेटिव के अनुपात की सीमा तक आने के लिए, क्योंकि पहले डेरिवेटिव के अनुपात की सीमा फॉर्म की अनिश्चितता है 0/0 या /∞।

उदाहरण 5 L'Hospital के नियम का उपयोग करके दो कार्यों के अनुपात की सीमा की गणना करें:

यहाँ L'Hospital का नियम दो बार लागू होता है, क्योंकि फलनों के अनुपात की सीमा और व्युत्पन्नों के अनुपात की सीमा दोनों ही रूप ∞/∞ की अनिश्चितता देते हैं।

उदाहरण 6गणना

यहाँ L'Hospital का नियम दो बार लागू होता है, क्योंकि दोनों कार्यों के अनुपात की सीमा और डेरिवेटिव के अनुपात की सीमा 0/0 के रूप की अनिश्चितता देती है।

उदाहरण 7गणना

यहां L'Hospital का नियम दो बार लागू होता है, क्योंकि दोनों कार्यों के अनुपात की सीमा और डेरिवेटिव के अनुपात की सीमा पहले फॉर्म की अनिश्चितता देते हैं - /∞, और फिर फॉर्म 0/0 की अनिश्चितता।

उदाहरण 8गणना

यहां L'Hospital का नियम दो बार लागू होता है, क्योंकि दोनों कार्यों के अनुपात की सीमा और डेरिवेटिव के अनुपात की सीमा पहले फॉर्म ∞/∞ की अनिश्चितता और फिर फॉर्म 0/0 की अनिश्चितता देते हैं।

ल'होपिटल का नियम स्वयं लागू करें और फिर समाधान देखें

उदाहरण 9गणना

संकेत। यहां आपको सीमा चिन्ह के तहत भावों के परिवर्तन पर सामान्य से थोड़ा अधिक फुसफुसाहट करनी होगी।

उदाहरण 10गणना

.

संकेत। यहां एल'होपिटल का नियम तीन बार लागू करना होगा।

फॉर्म की अनिश्चितताओं का प्रकटीकरण "अनंत से शून्य गुणा"

उदाहरण 11.गणना

(यहां हमने फॉर्म 0∙∞ की अनिश्चितता को फॉर्म ∞/∞ में बदल दिया है, क्योंकि

और फिर L'Hopital के नियमों को लागू किया)।

उदाहरण 12.गणना

.

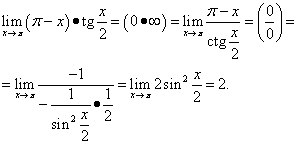
यह उदाहरण त्रिकोणमितीय पहचान का उपयोग करता है।

"शून्य की शक्ति के लिए शून्य", "शून्य की शक्ति के लिए अनंत" और "अनंत की शक्ति के लिए एक" प्रकार की अनिश्चितताओं का प्रकटीकरण

प्रपत्र की अनिश्चितता, या आमतौर पर प्रपत्र के किसी फ़ंक्शन के लघुगणक का उपयोग करके 0/0 या ∞/∞ के रूप में कम कर दी जाती है

व्यंजक की सीमा की गणना करने के लिए, का उपयोग करना चाहिए लघुगणकीय पहचान, जिसका एक विशेष मामला लघुगणक का गुण भी है .

लॉगरिदमिक पहचान और फ़ंक्शन की निरंतरता संपत्ति (सीमा के संकेत से परे जाने के लिए) का उपयोग करके, सीमा की गणना निम्नानुसार की जानी चाहिए:

अलग से, किसी को घातांक में व्यंजक की सीमा ज्ञात करनी चाहिए और निर्माण करना चाहिए इमिली डिग्री तक।

उदाहरण 13

.

.

उदाहरण 14एल अस्पताल के नियम का उपयोग करके गणना करें

.

.

उदाहरण 15एल अस्पताल के नियम का उपयोग करके गणना करें

घातांक में व्यंजक की सीमा की गणना करें

.

"इन्फिनिटी माइनस इनफिनिटी" फॉर्म की अनिश्चितताओं का प्रकटीकरण

ये ऐसे मामले हैं जहां कार्यों के अंतर की सीमा की गणना अनिश्चितता की ओर ले जाती है "इन्फिनिटी माइनस इनफिनिटी": .

L'Hopital के नियम के अनुसार ऐसी सीमा की गणना सामान्य दृष्टि सेनिम्नलिखित नुसार:

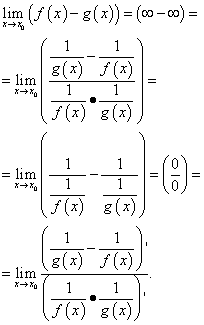
इन परिवर्तनों का परिणाम अक्सर होता है जटिल भाव, इसलिए, कार्यों के अंतर के ऐसे परिवर्तनों का उपयोग करने की सलाह दी जाती है जैसे कि एक सामान्य हर में कमी, गुणा और एक ही संख्या से भाग, उपयोग करें त्रिकोणमितीय पहचानआदि।

उदाहरण 16एल अस्पताल के नियम का उपयोग करके गणना करें

.

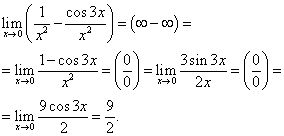
उदाहरण 17.एल अस्पताल के नियम का उपयोग करके गणना करें

.

लोपिटल नियम का उपयोग करके सीमाओं की गणना करें

अनिश्चितता भी या में बदलने का विरोध नहीं करती है:

एल अस्पताल के नियम

हम उस विषय को विकसित करना जारी रखते हैं, जिसे पेरिस एकेडमी ऑफ साइंसेज के सदस्य, मार्क्विस गुइल्यूम फ्रेंकोइस डी लोपिटल ने हमारे सामने रखा था। लेख एक स्पष्ट व्यावहारिक रंग प्राप्त करता है और काफी सामान्य कार्य में इसकी आवश्यकता होती है:

सिकुड़ने के क्रम में, हम संकेतक की सीमा की अलग से गणना करते हैं:

एक और पापुआन भी सूत्र के आगे हार मान लेता है। इस मामले में:

L'Hopital के नियम एक बहुत शक्तिशाली तरीका है जो आपको इन अनिश्चितताओं को जल्दी और प्रभावी ढंग से समाप्त करने की अनुमति देता है, यह कोई संयोग नहीं है कि समस्याओं के संग्रह में, परीक्षणों, परीक्षणों में, एक स्थिर टिकट अक्सर पाया जाता है: "सीमा की गणना करें, एल अस्पताल के नियम का उपयोग किए बिना". बोल्ड टाइप में आवश्यकता को स्पष्ट विवेक के साथ पाठ की किसी भी सीमा के लिए जिम्मेदार ठहराया जा सकता है सीमाएं। समाधान उदाहरण, उल्लेखनीय सीमाएं. हल करने के तरीके सीमित करें, उल्लेखनीय तुल्यता, जहां अनिश्चितता "शून्य से शून्य" या "अनंत से अनंत" होती है। भले ही कार्य संक्षेप में तैयार किया गया हो - "सीमाओं की गणना करें", तो यह स्पष्ट रूप से समझा जाता है कि आप अपनी पसंद की किसी भी चीज़ का उपयोग करेंगे, लेकिन L'Hospital के नियमों का नहीं।

कायापलट जारी है, अब "शून्य से शून्य" की अनिश्चितता सामने आ गई है। सिद्धांत रूप में, आप कोसाइन से यह संकेत देकर छुटकारा पा सकते हैं कि यह एकता की ओर जाता है। लेकिन एक बुद्धिमान रणनीति यह सुनिश्चित करना है कि कोई भी किसी भी चीज़ की तह तक न जाए। इसलिए, समस्या की स्थिति के अनुसार, हम तुरंत L'Hopital नियम लागू करते हैं:

के लिए एक समान कार्य स्वतंत्र निर्णय:

जैसा कि आप देख सकते हैं, अंश और हर के अंतर ने हमें आधे मोड़ के साथ उत्तर के लिए प्रेरित किया: हमें दो सरल डेरिवेटिव मिले, उनमें "दो" को प्रतिस्थापित किया गया, और यह पता चला कि अनिश्चितता बिना किसी निशान के गायब हो गई!

L'Hopital के नियम का उपयोग करके किसी फलन की सीमा ज्ञात कीजिए

बदले में, पीने वाले साथी और अधिक विदेशी साथियों को प्रकाश में खींच लिया जाता है। परिवर्तन विधि सरल और मानक है:

माना गया उदाहरण नष्ट हो जाता है और अद्भुत सीमाएं , इसी तरह के एक मामले पर लेख कॉम्प्लेक्स लिमिट्स के अंत में चर्चा की गई है।

मैं तुरंत आरक्षण कर दूंगा कि नियम संक्षिप्त "व्यावहारिक" रूप में दिए जाएंगे, और यदि आपको सिद्धांत पास करना है, तो मेरा सुझाव है कि आप अधिक कठोर गणनाओं के लिए पाठ्यपुस्तक की ओर रुख करें।

6) कमी के अंतिम नियम को दूसरी उल्लेखनीय सीमा पर लागू करें

अनिश्चितताओं के प्रकटीकरण को पहले चर्चा की गई अनिश्चितताओं तक सीमित कर दिया गया है। यदि, और पर, तो परिवर्तन लागू करें

अनंत या शून्य बटा शून्य L'Hopital के नियम का अनुप्रयोग है: दो . के अनुपात की सीमा

पिछली तीन अनिश्चितताओं के मामले में, परिवर्तनों को लागू किया जाना चाहिए

5) अनंत से अनंत तक के रूप की अनिश्चितता है।

अपरिमित रूप से छोटे या दो अपरिमित रूप से बड़े फलन उनके अवकलजों के अनुपात की सीमा के बराबर होते हैं,

3) अनिश्चितता को देखते हुए, पिछला नियम लागू करें

एल अस्पताल के नियम के अनुसार सीमाओं की गणना

उन कार्यों की सीमाओं की गणना करने का एक कुशल तरीका जिनमें अनंत प्रकार की विलक्षणताएं हैं

समाधान। 1) प्रतिस्थापन द्वारा, हम यह स्थापित करते हैं कि हमारे पास शून्य बटा शून्य के रूप की अनिश्चितता है। छुटकारा पाना

फिर से हमें फॉर्म की अनिश्चितता मिली और L'Hospital के नियम को फिर से लागू किया गया

2) पिछले उदाहरण की तरह, हमारे पास अनिश्चितता है। L'Hopital के नियम से, हम पाते हैं

L'Hopital के नियम के प्रयोग ने अनिश्चितताओं को प्रकट करने की सभी संभावनाओं को प्रदर्शित किया।

संख्या इस प्रकार चुनी जाती है कि समानता (1) संतुष्ट हो और इसलिए, . अत: अंतराल पर एक फलन के लिए

बिंदु x 0 के आसपास के क्षेत्र में, अर्थात। पर (x 0 ,x), कॉची प्रमेय की शर्तें फलनों f(x) और g(x) के लिए संतुष्ट हैं। इसलिए, एक बिंदु сО(x 0 , x) इस प्रकार है कि

ल अस्पताल का नियम

हालांकि, ऐसी स्थिति संभव है जब व्युत्पन्न मौजूद नहीं होने की स्थिति में फ़ंक्शन का बिंदु x 0 पर एक चरम होगा।

मान लें कि फ़ंक्शन बिंदु x 0 के पड़ोस में n गुना भिन्न है। आइए n-1 से अधिक नहीं डिग्री का बहुपद खोजें, जैसे कि

इसके अलावा, बिंदु x 0 को छोड़कर, बिंदु x 0 के कुछ पड़ोस में कार्य f(x) और g(x) निरंतर और भिन्न होने दें। होने देना, । फिर यदि फलनों के अवकलजों के अनुपात की सीमा होती है, तो स्वयं फलनों के अनुपात की भी एक सीमा होती है, और वे एक दूसरे के बराबर होते हैं, अर्थात्। .

निष्कर्ष: एक्सपोनेंशियल फंक्शन (y=a n) हमेशा पावर फंक्शन (y=x n) की तुलना में तेजी से बढ़ता है।

मैकलॉरिन सूत्र को लागू करने के एक उदाहरण के रूप में, आइए निर्दिष्ट सूत्र के अनुसार किसी फ़ंक्शन के विस्तार में शब्दों की संख्या निर्धारित करें ताकि अंतराल से किसी भी x के लिए 0.001 की सटीकता के साथ इसके मूल्य की गणना की जा सके [-1,1]।

परिभाषा:समारोह कहा जाता है गैर-घटता (गैर-बढ़ती)से (ए;बी) यदि किसी के लिए x 1 उपयोगी लेख में पोस्ट किया गया

L'Hopital के नियम के अनुसार किसी बिंदु पर किसी फलन की सीमा ज्ञात करना

L'Hopital के नियम के अनुसार, 0/0 और /∞ के रूप की अनिश्चितताओं को प्रकट करते हुए किसी फलन की सीमा ज्ञात करना।

नीचे कैलकुलेटर L'Hospital नियम (अंश और हर के व्युत्पन्न के माध्यम से) के अनुसार फ़ंक्शन की सीमा का पता लगाता है। नीचे नियम विवरण देखें।

किसी बिंदु पर फलन की सीमा - L'Hopital का नियम

मान्य संचालन: + - / * ^ स्थिरांक: pi कार्य: sin cosec cos tg ctg sec sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos Haversin exsec excsc sqrt sh ch th cth csch

ल अस्पताल का नियम

यदि निम्नलिखित शर्तें पूरी होती हैं:

• फलन f(x) और g(x) की सीमाएं एक दूसरे के बराबर और शून्य या अनंत के बराबर हैं:
  या;
• कार्य g(x) और f(x) पंचर पड़ोस a में अवकलनीय हैं;
• फ़ंक्शन का व्युत्पन्न g(x) पंचर पड़ोस में शून्य के बराबर नहीं है a
• और व्युत्पन्न f(x) और व्युत्पन्न g(x) के अनुपात की एक सीमा है:

तब फलनों f(x) और g(x) के अनुपात की एक सीमा होती है:
,

और यह फलन f(x) के अवकलज और फलन g(x) के अवकलज के अनुपात की सीमा के बराबर है:

सूत्र संख्या पीआई (पीआई), एक्सपोनेंट (ई), निम्नलिखित गणितीय ऑपरेटरों के उपयोग की अनुमति देता है:

+ - योग
— - घटाव
* - गुणन
/ - विभाजन
^ - घातांक

और निम्नलिखित विशेषताएं:

sqrt - वर्गमूल

जड़ पी- डिग्री रूट पी, उदाहरण के लिए root3(x) घनमूल है

expक्स्प - ई निर्दिष्ट शक्ति के लिए

एलबी - बेस 2 लॉगरिदम

एलजी - आधार 10 लघुगणक

एलएन- प्राकृतिक(ई पर आधारित)

लकड़ी का लट्ठा पी- आधार लघुगणक पी, उदाहरण के लिए log7(x) - आधार 7 लघुगणक

पाप - ज्या

कॉस - कोसाइन

टीजी - स्पर्शरेखा

सीटीजी - कोटैंजेंट

सेकंड - सेकंड

कोसेक - कोसेकेंट

आर्कसिन - आर्कसिन

आर्ककोस - चाप कोसाइन

आर्कटिक - चाप स्पर्शरेखा

arcctg - चाप स्पर्शरेखा

आर्कसेक - आर्कसेकेंट

आर्ककोसेक - आर्ककोसेकेंट

बनाम - बनाम

वर्कोस - कवरसिन

हावर्सिन - हावर्सिनस

एक्ससेक - एक्सेकेंट

एक्सएससी - एक्सोसैंट

श - अतिपरवलयिक ज्या

ch - अतिपरवलयिक कोज्या

वें - अतिपरवलयिक स्पर्शरेखा

सीटीएच - अतिपरवलयिक कोटैंजेंट

sec - अतिशयोक्तिपूर्ण secant

csch - अतिपरवलयिक कोसेकेंट

एब्स - निरपेक्ष मान (मापांक)

sgn - साइनम (चिह्न)

• एक ड्राइवर के बिना एक गज़ेल या सेबल वैन किराए पर लें गज़ेल-बिजनेस, 1 ड्राइवर + 2 यात्री। शरीर: 3 मीटर लंबाई, 2 मीटर ऊंचाई, बुटका। घन का आयतन 10.5. इंजन: UMZ-4216 (गैसोलीन), यूरो-4, 106.8 […]
• 2017-2018 में करों और योगदानों के भुगतान का विवरण 2017-2018 में करों के भुगतान का विवरण किसी भी भुगतान का एक अभिन्न अंग है। सही ढंग से भरें पेमेंट आर्डर […]
• अपनाया गया फेडरेशन काउंसिल द्वारा विचार करने की प्रक्रिया राज्य ड्यूमा संघीय कानून(अनुच्छेद 103-110) अनुच्छेद 103. विचार के लिए एक संघीय कानून को अपनाना […]
• फौजदारी कानून। सामान्य भाग आपराधिक कानून मानदंड एक आपराधिक कानून मानदंड राज्य द्वारा स्थापित आचरण का एक नियम है, जो […]
• एक बंधक पर देरी के लिए दंड का आकार सीमित है 24 जुलाई को, एक कानून लागू होगा जो गैर-पूर्ति या अनुचित पूर्ति के लिए दंड की राशि को सीमित करता है […]
• गंभीर परिस्थितियों के साथ हत्या सजा वर्तमान आपराधिक कानून के अनुसार, साधारण हत्या (रूसी संघ के आपराधिक संहिता के अनुच्छेद 105 का भाग 1) "एक कारावास से दंडनीय है […]

फॉर्म 0/0 या ∞/∞ की अनिश्चितताओं का प्रकटीकरण और गणना में उत्पन्न होने वाली कुछ अन्य अनिश्चितताएं सीमा L'Hospital के नियम (वास्तव में दो नियम और उन पर टिप्पणी) की सहायता से दो अतिसूक्ष्म या असीम रूप से बड़े कार्यों के संबंध को बहुत सरल बनाया गया है।

सार एल अस्पताल के नियम यह है कि उस स्थिति में जब दो अपरिमित रूप से छोटे या अपरिमित रूप से बड़े फलनों के अनुपातों की सीमा की गणना 0/0 या /∞ के रूप की अनिश्चितता देती है, दो फलनों के अनुपात की सीमा को सीमा द्वारा प्रतिस्थापित किया जा सकता है उनके का अनुपात डेरिवेटिवऔर इस प्रकार एक निश्चित परिणाम प्राप्त करें।

आइए, L'Hopital के नियमों के निरूपण की ओर बढ़ते हैं।

दो असीम रूप से छोटे मानों की सीमा के मामले के लिए L'Hopital का नियम. यदि कार्य एफ(एक्स) तथा जी(एक्स एकएक, और इस पड़ोस में जी"(एक्स एकएक दूसरे के बराबर और शून्य के बराबर

().

दो अपरिमित रूप से बड़ी मात्राओं की सीमा के मामले के लिए L'Hôpital का नियम. यदि कार्य एफ(एक्स) तथा जी(एक्स) बिंदु के कुछ पड़ोस में अवकलनीय हैं एक, बिंदु के संभावित अपवाद के साथ एक, और इस पड़ोस में जी"(एक्स)≠0 और यदि और यदि x के रूप में इन कार्यों की सीमा बिंदु पर फ़ंक्शन के मान की ओर जाती है एकएक दूसरे के बराबर और अनंत के बराबर

(),

तो इन कार्यों के अनुपात की सीमा उनके डेरिवेटिव के अनुपात की सीमा के बराबर है

().

दूसरे शब्दों में, फॉर्म 0/0 या ∞/∞ की अनिश्चितताओं के लिए, दो कार्यों के अनुपात की सीमा उनके डेरिवेटिव के अनुपात की सीमा के बराबर है, यदि बाद वाला मौजूद है (परिमित या अनंत)।

टिप्पणियां.

1. L'Hopital के नियम तब भी लागू होते हैं जब फंक्शन एफ(एक्स) तथा जी(एक्स) पर परिभाषित नहीं हैं एक्स = एक.

2. यदि, फलनों के व्युत्पन्नों के अनुपात की सीमा की गणना करते समय एफ(एक्स) तथा जी(एक्स) हम फिर से फॉर्म 0/0 या ∞/∞ की अनिश्चितता में आते हैं, तो L'Hopital के नियमों को बार-बार (कम से कम दो बार) लागू किया जाना चाहिए।

3. L'Hopital के नियम तब भी लागू होते हैं जब फलनों (x) का तर्क एक अपरिमित संख्या की ओर प्रवृत्त होता है एक, और अनंत तक ( एक्स → ∞).

अन्य प्रकार की अनिश्चितताओं को भी 0/0 और /∞ प्रकार की अनिश्चितताओं में कम किया जा सकता है।

"शून्य से विभाजित शून्य" और "अनंत से विभाजित अनंत" प्रकारों की अनिश्चितताओं का प्रकटीकरण

उदाहरण 1

एक्स=2 फॉर्म 0/0 की अनिश्चितता की ओर ले जाता है। इसलिए, प्रत्येक फ़ंक्शन का व्युत्पन्न और हम प्राप्त करते हैं

अंश में, बहुपद के व्युत्पन्न की गणना की गई थी, और हर में - एक जटिल लॉगरिदमिक फ़ंक्शन का व्युत्पन्न. अंतिम बराबर चिह्न से पहले, सामान्य सीमा, x के बजाय एक ड्यूस को प्रतिस्थापित करना।

उदाहरण 2 L'Hospital के नियम का उपयोग करके दो कार्यों के अनुपात की सीमा की गणना करें:

समाधान। किसी दिए गए मान फ़ंक्शन में प्रतिस्थापन एक्स

उदाहरण 3 L'Hospital के नियम का उपयोग करके दो कार्यों के अनुपात की सीमा की गणना करें:

समाधान। किसी दिए गए मान फ़ंक्शन में प्रतिस्थापन एक्स=0 फ़ॉर्म 0/0 की अनिश्चितता की ओर ले जाता है। इसलिए, हम अंश और हर में कार्यों के डेरिवेटिव की गणना करते हैं और प्राप्त करते हैं:

उदाहरण 4गणना

समाधान। किसी दिए गए फ़ंक्शन में x के बराबर प्लस अनंत के मान को प्रतिस्थापित करने से /∞ रूप की अनिश्चितता हो जाती है। इसलिए, हम L'Hopital का नियम लागू करते हैं:

टिप्पणी। आइए उन उदाहरणों पर चलते हैं जिनमें L'Hopital नियम को दो बार लागू करना पड़ता है, यानी दूसरे डेरिवेटिव के अनुपात की सीमा तक आने के लिए, क्योंकि पहले डेरिवेटिव के अनुपात की सीमा फॉर्म की अनिश्चितता है 0/0 या /∞।

ल'होपिटल का नियम स्वयं लागू करें और फिर समाधान देखें

फॉर्म की अनिश्चितताओं का प्रकटीकरण "अनंत से शून्य गुणा"

उदाहरण 12.गणना

.

समाधान। हम पाते हैं

यह उदाहरण त्रिकोणमितीय पहचान का उपयोग करता है।

"शून्य की शक्ति के लिए शून्य", "शून्य की शक्ति के लिए अनंत" और "अनंत की शक्ति के लिए एक" प्रकार की अनिश्चितताओं का प्रकटीकरण

प्रपत्र की अनिश्चितता, या आमतौर पर प्रपत्र के किसी फ़ंक्शन के लघुगणक का उपयोग करके 0/0 या ∞/∞ के रूप में कम कर दी जाती है

व्यंजक की सीमा की गणना करने के लिए, लघुगणकीय पहचान का उपयोग करना चाहिए, जिसका एक विशेष मामला लघुगणक की संपत्ति है .

लॉगरिदमिक पहचान और फ़ंक्शन की निरंतरता संपत्ति (सीमा के संकेत से परे जाने के लिए) का उपयोग करके, सीमा की गणना निम्नानुसार की जानी चाहिए:

अलग से, किसी को घातांक में व्यंजक की सीमा ज्ञात करनी चाहिए और निर्माण करना चाहिए इमिली डिग्री तक।

उदाहरण 13

समाधान। हम पाते हैं

.

.

उदाहरण 14एल अस्पताल के नियम का उपयोग करके गणना करें

समाधान। हम पाते हैं

घातांक में व्यंजक की सीमा की गणना करें

.

.

उदाहरण 15एल अस्पताल के नियम का उपयोग करके गणना करें

उभरी हुई आँखों वाली गौरैयों के झुंड की कल्पना करें। नहीं, यह गड़गड़ाहट नहीं है, यह तूफान नहीं है, यह भी नहीं है एक छोटा लड़काहाथ में गुलेल के साथ। यह सिर्फ इतना है कि एक विशाल, विशाल तोप का गोला चूजों की मोटी में उड़ जाता है। बिल्कुल लोपिटल नियमउन सीमाओं से निपटें जिनमें अनिश्चितता है या .

L'Hopital के नियम एक बहुत शक्तिशाली तरीका है जो आपको इन अनिश्चितताओं को जल्दी और प्रभावी ढंग से समाप्त करने की अनुमति देता है, यह कोई संयोग नहीं है कि समस्याओं के संग्रह में, परीक्षणों, परीक्षणों में, एक स्थिर टिकट अक्सर पाया जाता है: "सीमा की गणना करें, एल अस्पताल के नियम का उपयोग किए बिना". बोल्ड टाइप में आवश्यकता को स्पष्ट विवेक के साथ पाठ की किसी भी सीमा के लिए जिम्मेदार ठहराया जा सकता है सीमाएं। समाधान उदाहरण, उल्लेखनीय सीमाएं. हल करने के तरीके सीमित करें, उल्लेखनीय तुल्यता, जहां अनिश्चितता "शून्य से शून्य" या "अनंत से अनंत" होती है। भले ही कार्य संक्षेप में तैयार किया गया हो - "सीमाओं की गणना करें", तो यह स्पष्ट रूप से समझा जाता है कि आप अपनी पसंद की किसी भी चीज़ का उपयोग करेंगे, लेकिन L'Hospital के नियमों का नहीं।

कुल मिलाकर दो नियम हैं, और वे एक-दूसरे से बहुत मिलते-जुलते हैं, दोनों ही सार में और जिस तरह से उन्हें लागू किया जाता है। विषय पर प्रत्यक्ष उदाहरणों के अलावा, हम अतिरिक्त सामग्री का भी अध्ययन करेंगे जो गणितीय विश्लेषण के आगे के अध्ययन के दौरान उपयोगी होगी।

मैं तुरंत आरक्षण कर दूंगा कि नियम संक्षिप्त "व्यावहारिक" रूप में दिए जाएंगे, और यदि आपको सिद्धांत पास करना है, तो मेरा सुझाव है कि आप अधिक कठोर गणनाओं के लिए पाठ्यपुस्तक की ओर रुख करें।

एल अस्पताल का पहला नियम

उन कार्यों पर विचार करें जो असीम रूप से छोटाकिन्हीं बिंदुओं पर। अगर उनके रिश्ते की कोई सीमा है, तो अनिश्चितता को खत्म करने के लिए हम ले सकते हैं दो डेरिवेटिव- अंश से और हर से। जिसमें: , वह है ।

टिप्पणी : सीमा भी मौजूद होनी चाहिए, अन्यथा नियम लागू नहीं होता है।

ऊपर से क्या होता है?

सबसे पहले, आपको खोजने में सक्षम होने की आवश्यकता है कार्यों के व्युत्पन्नऔर बेहतर, बेहतर =)

दूसरा, डेरिवेटिव को अंश से अलग और हर से अलग से लिया जाता है। कृपया भागफल के विभेदीकरण के नियम से भ्रमित न हों !!!

और, तीसरा, "x" अनंत सहित कहीं भी प्रवृत्त हो सकता है - यदि केवल अनिश्चितता थी।

आइए पहले लेख के उदाहरण 5 पर वापस जाएं सीमा के बारे में, जिसने निम्नलिखित परिणाम उत्पन्न किया:

अनिश्चितता 0:0 के लिए, हम L'Hospital का पहला नियम लागू करते हैं:

जैसा कि आप देख सकते हैं, अंश और हर के अंतर ने हमें आधे मोड़ के साथ उत्तर के लिए प्रेरित किया: हमें दो सरल डेरिवेटिव मिले, उनमें "दो" को प्रतिस्थापित किया गया, और यह पता चला कि अनिश्चितता बिना किसी निशान के गायब हो गई!

यह असामान्य नहीं है जब L'Hopital के नियमों को क्रमिक रूप से दो या लागू करना पड़ता है बड़ी मात्राटाइम्स (यह दूसरे नियम पर भी लागू होता है)। आइए इसे एक रेट्रो शाम के लिए निकालें उदाहरण 2 पाठ अद्भुत सीमाओं के बारे में:

दो बैगेल चारपाई पर फिर से ठिठुर रहे हैं। आइए L'Hospital का नियम लागू करें:

कृपया ध्यान दें कि पहले चरण में हर लिया जाता है एक यौगिक समारोह का व्युत्पन्न. उसके बाद, हम कई मध्यवर्ती सरलीकरण करते हैं, विशेष रूप से, हम कोसाइन से छुटकारा पाते हैं, यह दर्शाता है कि यह एकता की ओर जाता है। अनिश्चितता को समाप्त नहीं किया गया है, इसलिए हम L'Hopital नियम को फिर से लागू करते हैं (दूसरी पंक्ति)।

मैंने विशेष रूप से आपके लिए थोड़ा आत्म-परीक्षण करने के लिए सबसे आसान उदाहरण नहीं चुना। यदि यह पूरी तरह से स्पष्ट नहीं है कि वे कैसे पाए गए डेरिवेटिव, आपको अपनी विभेदन तकनीक को मजबूत करना चाहिए, यदि आप कोसाइन ट्रिक को नहीं समझते हैं, तो कृपया वापस जाएं अद्भुत सीमाएं. मुझे नहीं देखता विशेष अर्थचरण-दर-चरण टिप्पणियों में, क्योंकि मैंने पहले ही डेरिवेटिव और सीमाओं के बारे में पर्याप्त विस्तार से बात की है। लेख की नवीनता स्वयं नियमों और कुछ तकनीकी समाधानों में निहित है।

जैसा कि पहले ही उल्लेख किया गया है, ज्यादातर मामलों में L'Hopital के नियमों का उपयोग करने की आवश्यकता नहीं है, लेकिन अक्सर समाधान की किसी न किसी जांच के लिए उनका उपयोग करने की सलाह दी जाती है। अक्सर, लेकिन हमेशा नहीं। इसलिए, उदाहरण के लिए, उस उदाहरण की जांच करना अधिक लाभदायक है जिसे अभी उपयोग करने पर विचार किया गया है अद्भुत समकक्ष.

ल'अस्पताल का दूसरा नियम

भाई-2 दो सोते हुए आठों से लड़ता है। इसी तरह:

रिश्तों की सीमा हो तो असीम रूप से बड़ाफलन बिंदु पर: , तो अनिश्चितता को समाप्त करने के लिए, हम ले सकते हैं दो व्युत्पन्न- अंश से अलग करें और हर से अलग करें। जिसमें: , वह है अंश और हर में अंतर करते समय, सीमा का मान नहीं बदलता है.

टिप्पणी : सीमा मौजूद होनी चाहिए

फिर से, विभिन्न . में व्यावहारिक उदाहरण मूल्य अलग हो सकता हैअनंत सहित। यह महत्वपूर्ण है कि अनिश्चितता हो।

आइए पहले पाठ का उदाहरण #3 देखें: . हम L'Hospital के दूसरे नियम का उपयोग करते हैं:

चूंकि हम दिग्गजों के बारे में बात कर रहे हैं, आइए दो विहित सीमाओं का विश्लेषण करें:

उदाहरण 1

सीमा की गणना करें

"साधारण" विधियों द्वारा उत्तर प्राप्त करना आसान नहीं है, इसलिए, अनिश्चितता "अनंत से अनंत" को प्रकट करने के लिए, हम L'Hopital नियम का उपयोग करते हैं:

इस तरह, रैखिक प्रकार्यएक से अधिक आधार वाले लघुगणक की तुलना में वृद्धि का एक उच्च क्रम( आदि।)। बेशक, उच्च शक्तियों में "x" भी ऐसे लघुगणक को "खींच" देगा। वास्तव में, फलन काफी धीमी गति से बढ़ता है और इसका अनुसूचीसमान "x" के सापेक्ष अधिक कोमल है।

उदाहरण 2

सीमा की गणना करें

एक और फीका फ्रेम। अनिश्चितता को खत्म करने के लिए, हम L'Hopital नियम का उपयोग करते हैं, इसके अलावा, लगातार दो बार:

एक घातांकीय फलन, जिसका आधार एक से अधिक है( आदि।) की तुलना में विकास का उच्च क्रम ऊर्जा समीकरणसकारात्मक डिग्री के साथ.

इसी तरह की सीमाओं का सामना करना पड़ता है पूर्ण कार्य अध्ययन, अर्थात्, खोजते समय रेखांकन का स्पर्शोन्मुख. कुछ टास्क में ये भी नजर आते हैं सिद्धांत संभावना. मैं आपको दो उदाहरणों पर विचार करने की सलाह देता हूं, यह उन कुछ मामलों में से एक है जब अंश और हर को अलग करने से बेहतर कुछ नहीं है।

आगे पाठ में, मैं L'Hopital के पहले और दूसरे नियम के बीच अंतर नहीं करूँगा, यह केवल लेख की संरचना के उद्देश्य से किया गया था। सामान्य तौर पर, मेरे दृष्टिकोण से, यह अधिक संख्या वाले गणितीय स्वयंसिद्धों, प्रमेयों, नियमों, गुणों के लिए कुछ हद तक हानिकारक है, क्योंकि "प्रमेय 19 के अनुसार कोरोलरी 3 के अनुसार ..." जैसे वाक्यांश केवल एक के ढांचे के भीतर सूचनात्मक हैं। या कोई अन्य पाठ्यपुस्तक। सूचना के एक अन्य स्रोत में, वही "अनुपालन 2 और प्रमेय 3" होगा। इस तरह के बयान केवल लेखकों के लिए ही औपचारिक और सुविधाजनक होते हैं। आदर्श रूप से, गणितीय तथ्य के सार को संदर्भित करना बेहतर है। अपवाद ऐतिहासिक रूप से स्थापित शब्द हैं, उदाहरण के लिए, पहली अद्भुत सीमाया दूसरी अद्भुत सीमा.

हम उस विषय को विकसित करना जारी रखते हैं, जिसे पेरिस एकेडमी ऑफ साइंसेज के सदस्य, मार्क्विस गुइल्यूम फ्रेंकोइस डी लोपिटल ने हमारे सामने रखा था। लेख एक स्पष्ट व्यावहारिक रंग प्राप्त करता है और काफी सामान्य कार्य में इसकी आवश्यकता होती है:

वार्म अप करने के लिए, आइए कुछ छोटी गौरैयों से निपटें:

उदाहरण 3

कोसाइन से छुटकारा पाकर सीमा को प्रारंभिक रूप से सरल बनाया जा सकता है, लेकिन हम इस शर्त के लिए सम्मान दिखाएंगे और तुरंत अंश और हर में अंतर करेंगे:

व्युत्पन्न खोजने की प्रक्रिया में, गैर-मानक कुछ भी नहीं है, उदाहरण के लिए, सामान्य भाजक का उपयोग किया जाता है विभेदीकरण नियमकाम करता है .

माना गया उदाहरण नष्ट हो जाता है और अद्भुत सीमाएं, इसी तरह के एक मामले पर लेख कॉम्प्लेक्स लिमिट्स के अंत में चर्चा की गई है।

उदाहरण 4

एल अस्पताल के नियम के अनुसार सीमा की गणना करें

यह स्वयं का उदाहरण है। अच्छा मजाक =)

एक विशिष्ट स्थिति तब होती है, जब विभेदन के बाद, तीन या चार मंजिला भिन्न प्राप्त होते हैं:

उदाहरण 5

L'Hospital के नियम का उपयोग करके सीमा की गणना करें

आवेदन के लिए भीख मांगना उल्लेखनीय तुल्यता, लेकिन पथ शर्त द्वारा हार्ड-कोडित है:

विभेदीकरण के बाद, मैं बहु-मंजिला अंश से छुटकारा पाने और अधिकतम सरलीकरण करने की दृढ़ता से अनुशंसा करता हूं. बेशक, अधिक उन्नत छात्र अंतिम चरण को छोड़ सकते हैं और तुरंत लिख सकते हैं: , लेकिन कुछ सीमाओं में उत्कृष्ट छात्र भी भ्रमित हो जाएंगे।

उदाहरण 6

L'Hospital के नियम का उपयोग करके सीमा की गणना करें

उदाहरण 7

L'Hospital के नियम का उपयोग करके सीमा की गणना करें

ये स्वयं सहायता उदाहरण हैं। उदाहरण 7 में, आप किसी भी चीज़ को सरल नहीं कर सकते, भिन्न में अंतर करने पर यह बहुत सरल हो जाती है। लेकिन उदाहरण 8 में, L'Hopital नियम को लागू करने के बाद, तीन मंजिला संरचना से छुटकारा पाना अत्यधिक वांछनीय है, क्योंकि गणना सबसे सुविधाजनक नहीं होगी। पूरा समाधानऔर पाठ के अंत में उत्तर। अगर आपको कोई परेशानी है - त्रिकोणमितीय तालिकाकी मदद।

और, सरलीकरण नितांत आवश्यक है, जब विभेदीकरण के बाद, अनिश्चितता सफाया नहीं.

उदाहरण 8

L'Hospital के नियम का उपयोग करके सीमा की गणना करें

जाओ:

दिलचस्प बात यह है कि पहले विभेदन के बाद की प्रारंभिक अनिश्चितता अनिश्चितता में बदल गई, और L'Hôpital का नियम आगे भी लागू होता है। यह भी ध्यान दें कि प्रत्येक "दृष्टिकोण" के बाद चार मंजिला अंश कैसे समाप्त हो जाता है, और स्थिरांक को सीमा चिह्न से बाहर कर दिया जाता है। सरल उदाहरणों में, स्थिरांक नहीं निकालना अधिक सुविधाजनक होता है, लेकिन जब सीमा जटिल होती है, तो हम सब कुछ-सब-सब कुछ सरल कर देते हैं। हल किए गए उदाहरण की कपटपूर्णता इस तथ्य में भी निहित है कि जब लेकिन, इसलिए, साइनस को खत्म करने के दौरान, संकेतों में भ्रमित होना आश्चर्यजनक नहीं है। अंतिम पंक्ति में, साइनस को नहीं मारा जा सकता था, लेकिन उदाहरण बल्कि भारी, क्षम्य है।

दूसरे दिन मेरे सामने एक दिलचस्प काम आया:

उदाहरण 9

सच कहूं तो मुझे थोड़ा शक हुआ कि यह सीमा किसके बराबर होगी। जैसा कि ऊपर दिखाया गया है, "x" लॉगरिदम की तुलना में विकास का एक उच्च क्रम है, लेकिन क्या यह क्यूबेड लॉगरिदम को "अधिक" करेगा? कौन जीतेगा, यह खुद जानने की कोशिश करें।

हाँ, ल'होपिटल के नियम न केवल तोप से गौरैयों पर गोली चलाना है, बल्कि श्रमसाध्य कार्य भी है ....

बैगेल्स या थके हुए आठों पर ल'होपिटल के नियमों को लागू करने के लिए, फॉर्म की अनिश्चितता कम हो जाती है।

अनिश्चितता से निपटने के बारे में पाठ के उदाहरण #9-13 में विस्तार से चर्चा की गई है। हल करने के तरीके सीमित करें. आइए इसके लिए एक और लें:

उदाहरण 10

L'Hopital के नियम का उपयोग करके किसी फलन की सीमा ज्ञात कीजिए

पहले चरण में, हम व्यंजक को एक सामान्य हर में लाते हैं, जिससे अनिश्चितता अनिश्चितता में बदल जाती है। और फिर हम L'Hopital नियम को चार्ज करते हैं:

यहाँ, वैसे, यह मामला है जब चार मंजिला अभिव्यक्ति को छूना व्यर्थ है।

अनिश्चितता भी या में बदलने का विरोध नहीं करती है:

उदाहरण 11

L'Hopital के नियम का उपयोग करके किसी फलन की सीमा ज्ञात कीजिए

यहां सीमा एकतरफा है, और इस तरह की सीमाओं पर पहले ही मैनुअल में चर्चा की जा चुकी है कार्यों के रेखांकन और गुण. जैसा कि आपको याद है, "शास्त्रीय" लघुगणक का ग्राफ अक्ष के बाईं ओर मौजूद नहीं है, इसलिए हम केवल दाईं ओर से शून्य तक पहुंच सकते हैं।

L'Hôpital के एक तरफा सीमा के नियम काम करते हैं, लेकिन अनिश्चितता से पहले निपटने की जरूरत है। पहले चरण में, हम अनिश्चितता प्राप्त करते हुए अंश को तीन मंजिला बनाते हैं, फिर समाधान टेम्पलेट योजना का अनुसरण करता है:

अंश और हर में अंतर करने के बाद, हम सरलीकरण करने के लिए चार मंजिला अंश से छुटकारा पाते हैं। नतीजतन, अनिश्चितता सामने आई। हम चाल को दोहराते हैं: हम फिर से भिन्न को तीन मंजिला बनाते हैं और परिणामी अनिश्चितता पर फिर से L'Hopital नियम लागू करते हैं:

तैयार।

कोई प्रारंभिक सीमा को दो डोनट्स तक कम करने का प्रयास कर सकता है:

लेकिन, सबसे पहले, हर में व्युत्पन्न अधिक कठिन है, और दूसरी बात, इससे कुछ भी अच्छा नहीं होगा।

इस तरह, समान उदाहरणों को हल करने से पहले, आपको विश्लेषण करने की आवश्यकता है(मौखिक रूप से या मसौदे पर) किस अनिश्चितता को कम करना अधिक लाभदायक है - "शून्य से शून्य" या "अनंत से अनंत" तक।

बदले में, पीने वाले साथी और अधिक विदेशी साथियों को प्रकाश में खींच लिया जाता है। परिवर्तन विधि सरल और मानक है।